Blogger
Fyrste julenøtt: panagram
desember 3, 2012 - 13:44 — Ragnar HaugeAssisterande forskningssjef Ragnar Hauge og seniorforskar Anders Løland
Eit pangram er ein meiningsfylt setning som nyttar alle bokstavane i eit språk. Eit døme er
«Quisling var ein kløppar til å spela jazz på xylofon, men lærte seg aldri å spela cembalo før han drog til Washington.»
Klassisk kvalitetsmåling av pangram er kor mange bokstavar dei har. For å unngå at folk berre går på nett og søker opp gode løysingar har vi vald eit anna kriterium:
• Alle bokstavar må brukast minst éin gong.
• Kvar bokstav som er brukt meir enn éin gong får ein kvadratisk straff: Å bruka ein bokstav to gongar gir ein straff på straff på 4, tre gongar ein straff på 9, og så vert det verre. Det er altså betre å bruka tre ulike bokstavar dobbelt enn å bruka éin bokstav tre gongar.
På norsk gir c, q, w, x og z ein del problem, så vi tillet særnamn.
Send inn ditt pangram, anten på bokmål eller nynorsk, til julekalender@nr.no innan torsdag 6. desember kl. 14. Vinnaren stikk av med attraktive NR-effektar.
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |
Gode sommerdekk?
mars 16, 2012 - 09:18 — Anders Løland
NAF har prisverdig nok også i år testet sommerdekk for oss. VG kan melde at «Nokian (Finland) og Pirelli (Italia) deler førsteplassen med Hankook - alle med 9,2 av 10 poeng».
Det stemmer sikkert, selv om slike tester også har et subjektivt element. Detaljene fra testen gjør NAF rede for på sitt eget nettsted.
Jeg gjengir for enkelhets skyld sluttresultatene per dekk:
Her kan vi for eksempel lese at vi bør holde oss unna BF Goodrich, som bare får 6,2 poeng, mot 9,2 poeng for de tre vinnerne. 9,2 er like under 10 og selv 6,2 poeng av 10 høres vel ikke så verst ut? I avveiningen mellom pris og nytte (der du har laget deg en såkalt nyttefunksjon), kan det godt være at BF Goodrich eller Jinyu er gode nok for deg, gitt at dekkene er billige nok.
Pussig nok er det ikke snakk om 9,2 eller 6,2 poeng av 10, men 6,2 på en skala fra 4 til 10 poeng (som NAF gjør oppmerksom på i sin tabelltekst). Det er derfor ikke mulig å få færre enn 4 poeng. Hvis vi derfor regner om poengene til prosent (hvor 0% er minimum og 100% er maksimum!) får vi en ny tabell:
Nå er det straks mye klarere hvor forskjellige dekkene er. Testens tre vinnere har et stykke opp til full score. De tre dårligste dekkene er ikke nokså gode, som NAFs poengskala ga inntrykk av. Valget mellom et dekk som scorer 6,2 poeng og 37 % er enkelt, problemet er at det er det samme dekket! Det kan forkludre kundens avveining mellom pris og kvalitet.
Den noe uvanlige poengskalaen over føyer seg inn i en god trikse-med-skala-tradisjon. Allerede i 1954 ga Darrell Huff ut «How to Lie with Statistics», som fortsatt selger godt.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
Sikker lottogevinst?
desember 14, 2011 - 15:16 — Ragnar HaugeNo som lykketallspotten er så stor, bør det vel løna seg å spela Viking Lotto? Så enkelt er det ikkje!
Når ein tipper lotto vil ein i gjennomsnitt få tilbake halvparten av innsatsen. Eit viktig unntak er pengar som vert flytta over frå forrige runde, som ved jackpot (førstepremiebeløpet går over til neste runde dersom ingen vinn førstepremie), eller lykketalspotten i Viking Lotto.
Spele alle rekkene?
Summen som er overført frå tidlegare i denne potten er på i overkant av 130 millionar. Å tippa alle rekkene kostar om lag 50 millionar, av dette får du igjen om lag halvparten, og med 130 millionar overført i tillegg ser det ut som om dette kan vera ei grei investering.
Fullt så enkelt er det likevel ikkje. Hovedgrunnen til det er at lykketallspotten ikkje er garantert. I kvar runde er det berre 1/8 sjanse for at den vert utbetalt, og om det ikkje skjer, har du tapt 25 millionar. I gjennomsnitt vil 16,5 millionar av potten verta utbetalt, så det er framleis eit forventa tap å spela alle rekkjer.
Er 200 millioner nok?
Så kor stor må lykketalspotten bli for at det skal vera interessant? Ei minste grense er 8 x 25 millionar = 200 millionar (sidan ein berre har 1/8 sjanse må beløpet vera 8 gonger så stort som det ein ynskjer å vinna). Men heller ikkje dette er nok, for potten vil verta delt mellom alle vinnarar av førstepremie.
Enorm lykketalspott!
Omsetjinga pleier å auka med storleiken på lykketalspotten, men la oss sjå bort frå det. Kanskje bruker folk alt dei kan på lotto allereie. I alle fall er omsetjinga no på nesten 150 millionar totalt i alle land som er med. Dette er før vi investerer 50 millionar, så det er i gjennomsnitt allereie 3 andre vinnarar der ute. Dermed vert berre 1/4 av potten vår, og beløpet må 4-doblast igjen for å bli interessant. Det vil seia ein lykketalspott på 800 millionar.
To identiske snøkrystallar?
Ein kan jo då lura på kor lenge det er til potten vert så stor. Slik det er no aukar potten med 4-5 millionar per veke. Dersom ein seier 5 millionar vil det seia at ein om 670/5 = 134 veker, eller altså drøyt to og eit halvt år kan byrja å tenkja på denne investeringa. Gitt at ingen har vunne lykketalspotten før det, sjølvsagt. Dessverre er det praktisk talt 100% sannsynlig at nokon gjer det - det er like sannsynleg at det har vore to identiske snøkrystallar på jorda som at lykketalspotten ikkje blir utbetalt i denne tida.
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |
Strekker Laban seg litt lengre?
september 28, 2011 - 12:59 — Bård Storvik Nidar har i deres kampanjer brukt følgende slagord ”Laban seigmenn strekker seg litt lengre”. Er det imidlertid virkelig slik at denne seigmanntypen kan strekkes lengre? Vi utførte strekkeksperimenter på seigmenn fra Nidar og Frist Price i forbindelse med Forskningstorget 2011 i Oslo med publikum som bidragsyter, for å kaste lys over spørsmålet.
Nidar har i deres kampanjer brukt følgende slagord ”Laban seigmenn strekker seg litt lengre”. Er det imidlertid virkelig slik at denne seigmanntypen kan strekkes lengre? Vi utførte strekkeksperimenter på seigmenn fra Nidar og Frist Price i forbindelse med Forskningstorget 2011 i Oslo med publikum som bidragsyter, for å kaste lys over spørsmålet.
I mange situasjoner både i hverdagen og innen vitenskapen kommer man over ulike former for påstander som ikke kan bekreftes direkte. For eksempel slik som her, hvor Nidar implisitt har påstått at deres seigmenn kan strekkes lengre enn andre seigmenn. Ofte finnes det ikke noen eksakt metode for å sjekke om påstanden er riktig eller gal. Det er da statistisk hypotesetesting kommer inn i bildet. Hypotesetesting er vitenskapens verktøy for å kunne si noe om det usikre. Ved å gjennomføre gjentatte forsøk, eller gjøre mange nok observasjoner av samme hendelse, kan man teste om en hypotese synes å holde eller ei.
Null-hypotesen
Påstanden eller hypotesen man ønsker å teste, kalles for null-hypotesen, og svarer typisk til det generelle standpunktet. I vårt tilfelle med seigmannstrekking har vi ikke noe generelt standpunkt. Vi tror heller ikke at Nidar har testet hypotesen vitenskaplig. Derfor er det rimelig å sette null-hypotesen til å være ”Laban og First Price seigmenn strekker seg like langt”. Dersom dataene klart tyder på at null-hypotesen ikke er sann, sier vi at den forkastes. Det er viktig å være klar over at dersom null-hypotesen ikke forkastes, så betyr ikke det nødvendigvis at den er sann, det er bare ikke nok som tyder på at den er usann. En test kan aldri bevise null-hypotesen, testen kan kun enten forkaste den eller ikke forkaste den.
Parallell til straffesaker
For å forstå dette kan det være nyttig å trekke en parallell til straffesaker i rettsapparatet. Null-hypotesen svarer til at tiltalte er uskyldig, mens alternativet er at vedkommende er skyldig. Bevisene kan ses på som data som blir samlet inn. Dersom bevisene ikke er sterke nok til at dommere og jury er klart overbevist om at tiltalte er skyldig, kan man ikke forkaste null-hypotesen, og dermed heller ikke dømme tiltalte. "Den tiltalte er uskyldig inntil det motsatte er bevist", er den ufravikelige regelen i rettssaker - det samme gjelder for hypotesetesting.
Bidrag fra publikum
I vårt strekkeksperiment på Forskningstorget i Oslo bidro publikum vitenskapelig ved å utføre strekking av to ulike typer seigmenn. Resultatet av eksperimentet ble fortløpende nedtegnet i en database og statistiske metoder ble brukt til å teste hypotesen. Etter hvert eksperiment fikk altså publikum tilbakemelding i form av en foreløpig konklusjon på gjeldende tidspunkt. Eksperimentene ble utført under de to dagene Forskningstorget i Oslo hadde boder ved Karl Johan. Responsen var svært god, mange var innom og en del elever var genuint interessert i å lære mer. Blant annet uttalte en elev: ”Nå skjønner jeg hva læreren prøvde å forklare om hypotesetesting”.

Når eksperimentene går galt
Det viste seg at seigmannstrekking var en hard prøvelse for våre strekkemaskiner, som i hovedsak bestod av en skrustikke med en festemekanisme. Sukkeret på seigmennene gjorde at gjengene på skrustikkene ble ødelagt og dermed måtte vi hjelpe til med å dra for å få målt strekklengden. Dette førte igjen til ujevn strekking. I tillegg gav noen av deltakerne inn resultater første dagen som ikke kunne stemme. Det var til tider temmelig kaotisk første dag med mange skoleelever som gjorde at vi ikke kunne følge opp enhver som leverte inn resultatene. Resultatene fra første dag viste at Laban strakk seg gjennomsnittlig litt lenger enn First Price sine seigmenn, men denne forskjellen var ikke signifikant, som betyr at det var for mye variasjon og for få eksperimenter til å trekke en konklusjon om at Laban strekker seg litt lengre. For å gjøre en vitenskaplig undersøkelse må eksperimentene være mest mulig like hver gang. Endring av type maskin kan gi forskjeller i resultater. Vi endret type maskin på andre dag og innså dermed muligheten for endring i resultater. På grunn av problemene vi hadde med strekkemaskiner, endring av strekkmaskin og feilregistreringer, ekskluderte vi eksperimentene fra første dag og brukte kun eksperimentene fra andre dag til å trekke en konklusjon.
Unike seigmenn
Hver seigmann er unik, så vi greier ikke å strekke hver seigmann av samme type eksakt like langt. Jo flere forsøk vi utfører, jo sikrere blir vi imidlertid på hvor stor den gjennomsnittlige differansen er mellom strekklengden til Nidar og First Price sine seigmenn.
Konklusjon
Alle rimelige tester vil vise at konklusjonen er at null-hypotesen ”Laban seigmenn og First Price seigmenn strekker seg like langt” forkastes og vi tror på alternativet ”Laban seigmenn strekker seg litt lengre”. Faktisk viste det seg at Laban seigmenn strakk seg gjennomsnittlig 0,67 cm lengre enn First Price seigmenn for de i alt 236*2=472 strekkeksperimenter. Den gjennomsnittlige strekklengden for Laban og First Price er henholdsvis 6,53 cm og 5,86 cm. Det er verdt å merke seg at strekklengdene er et resultat av vår strekkmetode. Andre faktorer slik som temperatur, lagringstid osv kan også spille inn. Den såkalte p-verdien var ekstremt liten, som betyr at vi er overbevist om at konklusjonen om å forkaste null-hypotesen er riktig.
Vi har kun testet ut Laban mot First Price seigmenn. Testing av andre typer seigmenn kan vise seg å endre konklusjon. I tillegg kan andre strekkteknikker føre til andre strekklengder.
| Bård Storvik |
Jeg har vært ansatt på Norsk Regnesentral (NR) siden 1999. I 1991 tok jeg hovedfag og senere i 2000 doktorgrad i statistikk ved Universitet i Oslo. På NR har jeg vært innom veldig mange områder. Noen av disse områdene inkluderer system for optimal leveranse av aviser for Dagbladet, løpende utvalgsundersøkelse om kopiering i universitets- og høgskolesektoren for Kopinor, modellering av misligholdssannsynligheter for Pareto, sannsynlighetsvurderinger av førstepremie knyttet til spillet JOKER, system for beregning av tid det tar å bore en brønn for Hydro/Statoil og modellering av ulike laksesykdommer innen oppdrettsnæringen i samarbeid med Veterinærinstituttet. På fritiden bruker jeg mye tid på å trene og da særlig badminton. |
Friidretts-VM: Lurt å være god og ustabil!
september 2, 2011 - 16:04 — Frode Georgsen
I disse dager samles verdenseliten i friidrett i Daegu i Sør-Korea for å kjempe om tittelen «verdensmester» i ulike grener. For statistikere er friidrett en drømmeidrett med nesten ubegrenset tilgang på tall og statistiker. Norges eneste reelle gullhåp er spydkaster Andreas Thorkildsen. Siden han slo igjennom i OL i Athen i 2004, har han stort sett levert varene med 2 OL-gull, 2 EM-gull og 1 VM-gull. Thorkildsen har vunnet så mye i disse årene fordi han har vært den kasteren med det høyeste nivået. Et høyt gjennomsnittsnivå vil imidlertid ikke nødvendigvis føre til seier.
Det spesielle med kastøvelsene, og også lengde og tresteg, er at det ikke er stabilitet og gjennomsnittsresultat som er avgjørende. Den som har det ene lengste kastet (eller hoppet) av seks forsøk vinner, uavhengig av resultat i de andre forsøkene. (Vi ser for enkelthets skyld bort fra at utøverne i et mesterskap må gjennom kvalifisering og at de må sørge for å være blant de åtte beste etter tre forsøk for å få fullføre.) Gitt et bestemt gjennomsnittsnivå, er det da ideelt å ha størst mulig spredning i resultatene. Med andre ord; det er lurt å være god og ustabil.
Best av seks
Vi kan se på resultatet i denne type konkurranser som den maksimalt oppnådde lengden av seks uavhengige forsøk. Lengden i hvert forsøk følger en sannsynlighetsfordeling med en forventning (gjennomsnittsresultat over tid) og et standardavvik (spredning rundt gjennomsnittsresultatet). Denne sannsynlighetsfordelingen kan for eksempel være normalfordelingen, som følger den kjente Gausskurven.
Da Andreas Thorkildsen i fjor vant EM i Barcelona, hadde han ikke det beste gjennomsnittsresultatet (85,72 meter mot Matthias De Zordo med 86,30 meter), og hans nest beste kast var bare konkurransens 5. beste. Men han vant likevel fordi han hadde det lengste kastet på 88,37 meter. Ser vi på spredningen i Thorkildsens fem gyldige kast var standardavviket på 1,98 meter, mens De Zordo hadde 1,59 meter. Et høyt standardavvik tilsier at sjansen for å kaste dårlig er større, men det er også sjansen for et skikkelig langt kast. Det kan være nok for å vinne heder, ære og gull.
Thorkildsen over 90 meter?
Ser vi på alle OL, VM og EM fra 2004 til nå, har Andreas Thorkildsen gjennomsnittlig kastet 85,36 meter. Dersom vi sier at dette er et rimelig anslag på hans forventede resultat i et enkelt kast, vil vi også være interessert i spredningen. Med et standardavvik på 0, vil sluttresultatet garantert bli 85,36 meter. Det vil sannsynligvis ikke holde til gull. Nå har Andreas Thorkildsen faktisk et standardavvik i løpet av perioden på 3,07 meter. Sannsynligheten for at han da skal klare 90 meter i løpet av seks kast er 33%. Ingen andre i verden har kastet så langt i år. Thorkildsens argeste konkurrent i perioden 2004-2011, finske Tero Pitkämäki, har et lavere gjennomsnittsresultat (83,12 meter), men han kan håpe at hans litt høyere ustabilitet skal hjelpe ham (standardavvik på 3,16 meter). Dette er bare marginalt bedre enn Andreas Thorkildsen, og hans sannsynlighet for å kaste 90 meter er kun 10%. Vel så interessant er sannsynligheten for at Tero Pitkämäki slår Andreas Thorkildsen. Denne er på 22%.
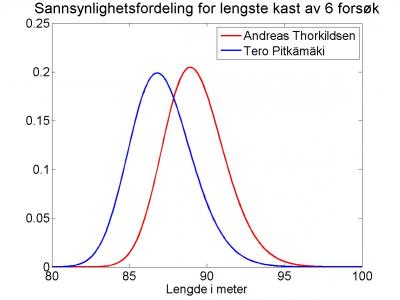
Figuren viser sannsynlighetsfordelingen for sluttresultatet (det lengste kastet) av seks forsøk for henholdsvis Andreas Thorkildsen og Tero Pitkämäki. Ser man nøye på den, ser man at den ikke følger en symmetrisk Gausskurve, men har et tyngdepunkt litt forskjøvet mot høyre.
Ved å ta med historiske resultater for flere utøvere, vil man se at Andreas Thorkildsen ofte vinner ikke bare fordi han er god, men også fordi han er blant de med størst spredning i kastlengdene.
Den enkle analysen over kan utvides ved for eksempel å ta hensyn til sannsynligheten for ugyldig kast, eller at utøverne blir slitne utover i konkurransen.
Heldigvis for oss som liker spennende sport, skal konkurransen avgjøres på banen og ikke via datamaskinens beregninger av matematiske modeller. Dermed kan (nesten) alt skje.

| Frode Georgsen | Jeg er seniorforsker ved Norsk Regnesentral og jobber på den avdelingen (SAND) som driver med statistisk og matematisk modellering av geologi i olje- og gassreservoarer. Jeg er utdannet statistiker ved Universitetet i Oslo. I tillegg spiller jeg tuba og er sportsidiot. Spesielt er jeg interessert i skøyter og friidrett, og liker å se på sport på toppnivå og utøve sport på middelmådig nivå. Disse interessene må imidlertid tilpasses til at jeg også er gift og har tre barn. |




