Innovasjon og statistisk modellering i offentlig sektor
oktober 11, 2010 - 17:13 — André TeiglandEtter mange år som forskningssjef for statistikkmiljøet ved Norsk Regnesentral, noterer jeg meg at de aller fleste av våre oppdragsgivere (eller kunder om man vil) er private. Ikke dermed sagt at vi ikke har offentlige kunder, vi har blant annet oppdrag for Vegdirektoratet, Tollvesenet, Skatteetaten og NAV, men det er et faktum at det aller meste av våre inntekter kommer fra private aktører. Hvorfor er det slik?
Prognoser, risikoanalyser, mønstergjenkjenning, statistiske analyser, forståelse av usikkerhet, modellering, fremskrivninger. Listen over problemstillinger vi arbeider med for private aktører er lang. Er disse problemstillingene mindre interessante for offentlig sektor, hvor det tas mange og viktige beslutninger basert på ulike data? Jeg mener bestemt nei. Er vi dårligere til å selge vår kompetanse til det offentlige? Det er mulig, men er det også andre utfordringer som begrenser samarbeidet?
Uten at jeg skal påberope meg å kjenne den fulle sannhet, så er mitt inntrykk at mange av de modelleringsorienterte forskningsinstituttene gjør mest arbeid for privat sektor. Nå er det for så vidt ikke noe galt i det. At private aktører vil bruke sine penger på oss, må jo bety at vi gjør noe nyttig.
Likevel undres jeg altså på om vi ikke kunne gjort mer nytte for samfunnet. At det offentlige kjøper inn store mengder konsulentkompetanse er det jo lite tvil om. Men altså ikke så mye anvendt forskning, i hvert fall ikke innen statistisk modellering. Her kan jeg selvfølgelig lett beskyldes for å gråte for min syke mor, men jeg gjør egentlig ikke det (i hvert fall ikke så mye), statistikkmiljøet på NR går økonomisk meget bra det, med masse spennende prosjekter.
Det er to svært viktige faktorer som kjennetegner de aller fleste av våre mest vellykkede prosjektporteføljer for privat sektor; muligheten til i fellesskap med kunden å definere prosjektets ambisjoner, målsetting og omfang, samt langsiktige samarbeidsforhold.
Ligger noe av utfordringen her? Som skattebetaler setter jeg pris på at vi har en lov om offentlig anskaffelse, men egner anbudsprosessene seg for innkjøp av anvendt forskning? Jeg har begynt å tvile. I anvendt forskning vet man for eksempel ikke alltid hvor mye informasjon det ligger i dataene man ønsker å benytte. En klar svakhet ved anbudsprosessene er at oppdragsgiver normalt fullspesifiserer oppdraget på egenhånd, før den som skal løse problemet trekkes inn i bildet. Ofte ser vi at det som ønskes er urealistisk. Noen ganger ser vi at ved å omformulere oppdraget noe, ville man fått en mye bedre løsning. Denne problemspesifikasjonsfasen av et prosjekt er svært viktig i vår dialog med private aktører, mens den stort sett er fraværende i offentlige anbudsprosesser. Er det rom for å gjøre dette annerledes?
Hva med finansiering? Forskningsrådet har lenge hatt såkalte BIP’er (brukerstyrte innovasjonsprosjekter), der næringslivet kan få økonomisk risikoavlastning i prosjekter med en stor grad av forskning. Nå utvides tilbudet mot offentlig sektor også. Tilsvarende har Innovasjon Norge kontrakter for offentlig forskning og utvikling.
Forskningsinstituttene er høykompetansemiljøer som skal levere høykvalitet. Ut fra min erfaring tillater jeg meg å stille spørsmålet om man tillegger pris for stor vekt kontra kvalitet i offentlig sektor? Eller er instituttene for dyre? Offentlige midler skal brukes fornuftig, men jeg konstaterer at våre private kunder veier pris, nytte og kvalitet annerledes, og det er neppe fordi de ikke er opptatt av økonomi.
Sammen med Forskningsrådet og andre teknisk-industrielle institutter ønsker vi å se nærmere på bruk av forskning i det offentlige på seminaret ”Innovasjon i offentlig sektor med forskningsbaserte modeller” 22. oktober. Vel møtt!
| André Teigland |
Foto: Lin Stenstrud Jeg er forskningssjef og assisterende direktør ved Norsk Regnesentral, hvor jeg leder avdelingen Statistisk Analyse, Mønstergjenkjenning og Bildeanalyse. En stor del av jobben min består i å være med på utformingen av prosjektene våre i dialog med våre oppdragsgivere. Gjennom dette har jeg vært så heldig å få lang erfaring i å se hvordan metodefag som statistikk og bildeanalyse kan brukes til praktisk nytte på en rekke felt, noe jeg brenner for. Min utdannelse har jeg fra Universitetet i Oslo, hvor jeg tok hovedfag i statistikk i 1992. I alle år siden har jeg jobbet på NR, både som forsker og forskningssjef. Med en bakgrunn som fotballspiller, er jeg tilnærmet sportsidiot og en ivrig treningsmosjonist på ski eller sykkel. Ellers går mye av fritiden til å følge opp mine to barn og alle deres gjøremål. Heldigvis trives de like godt som meg i min kjære seilbåt! |
Petroleumsgeofysikerens Røst
oktober 11, 2010 - 08:50 — Heidi KjønsbergFor en stund siden deltok jeg på Lofoten-seminaret i Petroleumsgeofysikk. Det var en hyggelig seanse. For det første er Røst et spesielt, vakkert og levedyktig samfunn, men viktigst i denne sammenhengen var at seminarets opplegg og faglige innhold var rikholdig og variert. Her var det doktorgradsstudenter, professorer, forskere fra ulike institutter og bedrifter i den private sektor, og også representanter fra den offentlige forvaltning. Temaene favnet et vidt spenn, fra CO2-injeksjon på Snøhvit, via seimisk prosessering, sensitivitet av geofysiske parametre, Lofoten og Vesterålens geologi, til den ganske så vidløftige idéen om å bruke solitoner til å øke gjennomstrømningskapasiteten i oljefelt. Og mer. Et vidt spekter, virkelig!
Jeg synes det er svært positivt at det arrangeres seminarer og konferanser som gir god mulighet for å møte folk fra et norsk fagmiljø. Utenlandske konferanser er flott og viktig, men la meg denne gangen slå et slag for de nasjonale møtepunktene. Alle trenger et faglig nettverk, og for Norge er det viktig at det eksisterer en norsk forankring mange føler seg hjemme i. Hurra for Lofotenseminaret i Petroleumsgeofysikk!
Dette bildet av seminardeltakerne på geologiekskursjon er tatt fra UniGeos hjemmeside, det var de som arrangerte seminaret.

| Heidi Kjønsberg |
Jeg har jobbet på NR siden 2005, og er seniorforsker i avdelinga for Statistical Analysis of Natural Resource Data. Utdanninga mi har jeg fra Universitetet i Oslo, med en doktorgrad i teoretisk fysikk fra 1998. Jeg har jobbet med kvantefysikk, som forsker i telecom-industrien, og siden jeg startet på NR med matematisk modellering av olje- og gassreservoarer. På fritida lager jeg ofte mye og ganske god mat. Men gjester må finne seg i eksperimentering og tildels mye chili. Jeg liker fysisk arbeid, og holder på å lære meg å gjenkjenne fuglearter fra lyd og utseende. |
600 sparket av seg skoa og forsket med oss!
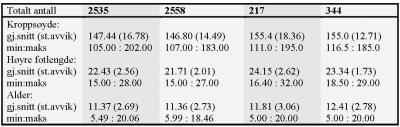
oktober 5, 2010 - 09:45 — Ingunn Fride Tvete Den 24. og 25. september gikk de årlige Forskningsdagene av stabelen over hele Norge. Norsk Regnesentral var som vanlig på plass på Universitetsplassen i Oslo. Tross kaldt vær og pøsregn tok mange turen innom Universitetsplassen i år også. I NRs bod kunne man måle fotlengden og kroppshøyden, og få analysert sine resultater sammen med andres. Vi er svært fornøyde med at nesten 600 mennesker stakk innom! Det var flest jenter/kvinner som fikk målt seg; hele 365 mot 213 gutter/menn. Det var et godt aldersspenn på deltagerne, den yngste bare 3 år og den eldste hele 81 år. Matematikkstudenten Kristina Rognlien Dahl, som har hatt sommerjobb hos Norsk Regnesentral, hadde på forhånd bygd opp en database med 250 personer. Til sammen har vi dermed målt fotlengden og kroppshøyden til nesten 850 personer.
Den 24. og 25. september gikk de årlige Forskningsdagene av stabelen over hele Norge. Norsk Regnesentral var som vanlig på plass på Universitetsplassen i Oslo. Tross kaldt vær og pøsregn tok mange turen innom Universitetsplassen i år også. I NRs bod kunne man måle fotlengden og kroppshøyden, og få analysert sine resultater sammen med andres. Vi er svært fornøyde med at nesten 600 mennesker stakk innom! Det var flest jenter/kvinner som fikk målt seg; hele 365 mot 213 gutter/menn. Det var et godt aldersspenn på deltagerne, den yngste bare 3 år og den eldste hele 81 år. Matematikkstudenten Kristina Rognlien Dahl, som har hatt sommerjobb hos Norsk Regnesentral, hadde på forhånd bygd opp en database med 250 personer. Til sammen har vi dermed målt fotlengden og kroppshøyden til nesten 850 personer.
Formålet med undersøkelsen vår var å illustrere hvordan statistisk analyse kan brukes, til for eksempel å beskrive sammenhengen mellom fotlengde og kroppshøyde. Dette har vært belyst i en rekke sammenhenger tidligere. Ingrid H. E. Rutishauser publiserte allerede in 1968 artikkelen Prediction of Height from Foot Length: Use of Measurement in Field Surveys. I studier av store populasjoner er det svært tidkrevende å måle kroppshøyden til alle deltagerne, mens det er mye raskere å ta et fotavtrykk. Rutishauser ønsket derfor å undersøke hvor pålitelig et fotavtrykkmål er for å anslå kroppshøyden. I hennes studie av vestafrikanske barn fant hun en sterk sammenheng mellom de to målene.
Rutishauser anslo en lineær sammenheng mellom fotlengde og kroppshøyde for årskull. Rent praktisk betyr dette å finne den linja som beskriver sammenhengen mellom fotlengdene og kroppshøydene best mulig. Dette kalles lineær regresjon. Med det som kalles minste kvadraters metode, finner man den rette linja som er slik at kvadratene av den vertikale forskjellen mellom linja og datapunktene man vil tilnærme er minst mulig.
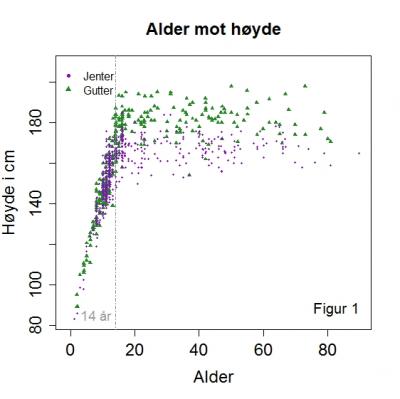 Vi har sett på sammenhengen mellom de målte fotlengdene og kroppshøydene på Forskningsdagene, der vi også tok hensyn til kjønn og alder på deltagerne. Figur 1 viser deltagernes alder mot høyde, der jentene er lilla prikker, mens guttene er grønne trekanter. Ikke uventet ser vi en trend med økende kroppshøyde ved økende alder frem til 15-årsalderen. Fra og med 15-årsalderen flater trenden ut, med en temmelig stor spredning i kroppshøyde for alle aldre.
Vi har sett på sammenhengen mellom de målte fotlengdene og kroppshøydene på Forskningsdagene, der vi også tok hensyn til kjønn og alder på deltagerne. Figur 1 viser deltagernes alder mot høyde, der jentene er lilla prikker, mens guttene er grønne trekanter. Ikke uventet ser vi en trend med økende kroppshøyde ved økende alder frem til 15-årsalderen. Fra og med 15-årsalderen flater trenden ut, med en temmelig stor spredning i kroppshøyde for alle aldre.
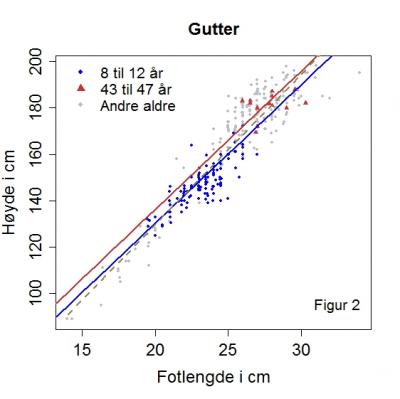 Vi har plottet fotlengden mot kroppshøyden for gutter og jenter i henholdsvis figur 2 og 3. Vi ser i begge figurene en økende kroppshøyde ved økende fotlengde. Man kan finne den linja som best beskriver sammenhengen, uten å ta hensyn til alder, og dette er vist ved den grå stiplede linjen. Som vi så i figur 1,varierer høyden med alder, spesielt for barn og unge. Det synes derfor naturlig å ta hensyn til alder når vi skal finne den linja som beskriver sammenhengen best. Man lar da kroppshøyden være en funksjon av både fotlengde og alder.
Vi har plottet fotlengden mot kroppshøyden for gutter og jenter i henholdsvis figur 2 og 3. Vi ser i begge figurene en økende kroppshøyde ved økende fotlengde. Man kan finne den linja som best beskriver sammenhengen, uten å ta hensyn til alder, og dette er vist ved den grå stiplede linjen. Som vi så i figur 1,varierer høyden med alder, spesielt for barn og unge. Det synes derfor naturlig å ta hensyn til alder når vi skal finne den linja som beskriver sammenhengen best. Man lar da kroppshøyden være en funksjon av både fotlengde og alder.
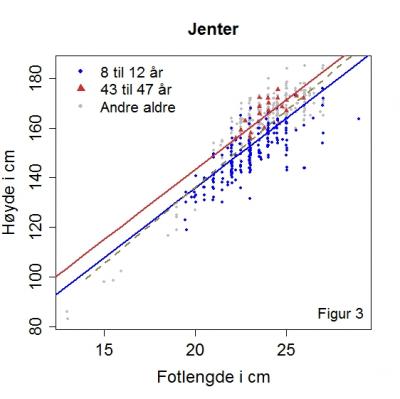 Man kan så vise den linja som beskriver sammenhengen best for ulike aldre. Dette har vi gjort for 10-åringer (blå linje) og 45-åringer (rød linje), for gutter i figur 2 og jenter i figur 3. Vi har markert alle fotlengde- og kroppslengdemålene med blå sirkler for 10-åringer +/- 2 år og med røde trekanter for 45-åringer +/- 2 år (de grå sirklene er altså alle de andre).
Man kan så vise den linja som beskriver sammenhengen best for ulike aldre. Dette har vi gjort for 10-åringer (blå linje) og 45-åringer (rød linje), for gutter i figur 2 og jenter i figur 3. Vi har markert alle fotlengde- og kroppslengdemålene med blå sirkler for 10-åringer +/- 2 år og med røde trekanter for 45-åringer +/- 2 år (de grå sirklene er altså alle de andre).
Theodoros B. Grivas med flere studerte sammenhengen mellom fotlengde og kroppshøyde for 5-20-åringer i Hellas i artikkelen Correlation of foot length with height and weight in school age children. De kom fram til følgende sammenheng mellom fotlengde og kroppshøyde når man tar hensyn til alder og kjønn:
Høyde i cm = 34.1 + 3.7 * Lengde høyre fot i cm + 1.6 (hvis jente) + 2.5 * alder i år
La oss nå gjøre samme analyse med våre norske 5-20 åringer. Oppsummerende måleresultater for grekerne og nordmennene er angitt i tabellen nederst på siden. Vi estimerer sammenhengen mellom fotlengde og kroppshøyde, når vi tar hensyn til alder og kjønn, på samme måte som Grivas med flere gjorde, men basert på våre data, og får:
Høyde i cm = 31.7 + 3.9 * Lengde høyre fot i cm + 1.3 (hvis jente) + 2.5 * alder i år
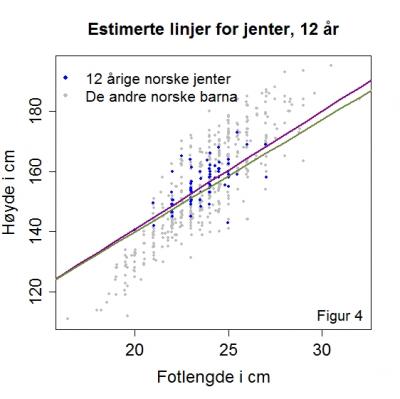 Vi ser at vår tilpassede modell er nokså lik den Grivas med flere fant. Vi kan plotte den estimerte linja for 12-årige jenter. Dette er gjort i figur 4. Her er den lilla linja den estimerte linja basert på våre data, mens den grønne linja er tilsvarende basert på greske data. Vi ser at den norske modellen anslår en noe høyere økning i kroppshøyde med økende fotlengde enn den greske. Mer presist, med den norske modellen anslår man en økning på 3,9 cm i kroppshøyde per økt cm i fotlengde, mens det tilsvarende tallet med den greske modellen er 3.7. Betydningen av alder er anslått til den samme, mens med den greske modellen får man estimert en økning i kroppshøyde på 1.6 cm for jenter sammenlignet med gutter, mens det tilsvarende tallet for den norske modellen er noe lavere, 1,3 cm. Basert på våre innsamlede fotlengder og kroppshøyder for barn og unge kan det altså se ut til at sammenhengen mellom disse to kroppsmålene ikke er veldig forskjellig i Hellas og Norge.
Vi ser at vår tilpassede modell er nokså lik den Grivas med flere fant. Vi kan plotte den estimerte linja for 12-årige jenter. Dette er gjort i figur 4. Her er den lilla linja den estimerte linja basert på våre data, mens den grønne linja er tilsvarende basert på greske data. Vi ser at den norske modellen anslår en noe høyere økning i kroppshøyde med økende fotlengde enn den greske. Mer presist, med den norske modellen anslår man en økning på 3,9 cm i kroppshøyde per økt cm i fotlengde, mens det tilsvarende tallet med den greske modellen er 3.7. Betydningen av alder er anslått til den samme, mens med den greske modellen får man estimert en økning i kroppshøyde på 1.6 cm for jenter sammenlignet med gutter, mens det tilsvarende tallet for den norske modellen er noe lavere, 1,3 cm. Basert på våre innsamlede fotlengder og kroppshøyder for barn og unge kan det altså se ut til at sammenhengen mellom disse to kroppsmålene ikke er veldig forskjellig i Hellas og Norge.
Når man ser på figurene kan man spørre seg om det er riktig å anta en lineær sammenheng. Hvordan man skal beskrive sammenhengen er ikke opplagt, og vi hadde mange interessante diskusjoner på Universitetsplassen. Jeg vil med dette benytte anledningen til å takke alle som kom innom boden vår denne gangen. Uten dere forskere kunne vi ikke gjort vår analyse!
NB: Som opplyst på arket alle deltagerne fikk med seg på Forskningsdagene: alle opplysningene som ble innhentet ble registret anonymt, ingen navn ble registrert, og dataene vil ikke bli brukt i noen annen sammenheng.
Referanser:
Rutishauser, I.H.E. Prediction of Height from Foot Length: Use of Measurement in Field Surveys. Archives of Disease in Childhood, 43 (1968) 310-312.
Grivas. T.B., Mihas, C., Arapaki, A. and Vasiliadis, E. Correlation of foot length with height and weight in school age children. Journal of Forensic and Legal Medicine, 15 (2008) 89ó95.
| Ingunn Fride Tvete |
Jeg har vært ansatt på NR siden 2000. Jeg tok hovedfag i forsikringsmatematikk på Blindern i 2000, og doktorgrad i statistikk i 2006 på samme sted. Jeg har den siste tiden jobbet mest med helserelaterte problemstillinger, blant annet med analyser av reseptregisterdata og antibiotikaresistensproblematikken. Jeg driver også en del med metaanalyser, der man kombinerer resultater fra flere studier for å undersøke en eller flere sammenhenger. På fritiden min løper jeg mest, baker en del kaker, syr klær og quilter litt. |
Spark av deg skoa og forsk med oss!
september 20, 2010 - 14:02 — Ingunn Fride Tvete Det er ekstra viktig å velge riktig størrelse når man handler klær på nettet. Har du kanskje holdt fast poden mens du fortvilt prøvde å legge målbåndet på kryss og tvers av den viltre kroppen? Det har kanskje hendt at du har funnet ut at barnet har for lange bein i forhold til overkroppen for den fine parkdressen du har sett deg ut? Du visste kanskje ikke at bak standardiserte avstandsmål av denne typen ligger det statistiske analyser?
Det er ekstra viktig å velge riktig størrelse når man handler klær på nettet. Har du kanskje holdt fast poden mens du fortvilt prøvde å legge målbåndet på kryss og tvers av den viltre kroppen? Det har kanskje hendt at du har funnet ut at barnet har for lange bein i forhold til overkroppen for den fine parkdressen du har sett deg ut? Du visste kanskje ikke at bak standardiserte avstandsmål av denne typen ligger det statistiske analyser?
Antropometri er læren om kroppsmålene. Man måler lengden på ulike deler av kroppen og beregner avstander og sammenhengen mellom ulike avstander. For eksempel er vanligvis kroppshøyden lik avstanden fra fingertupp til fingertupp. Denne typen kunnskap er nyttig når man skal designe møbler, biler, klær og sko. Forholdene mellom ulike kroppsmål kan variere litt fra verdensdel til verdensdel. Derfor kan det hende at klær du bestiller på nettet fra Asia ikke helt passer deg. Men kroppsmålene vil jo også variere litt fra person til person. En av mine grandonkler, som var kjent for spesielt lange bein, snekret på 50-tallet lenestoler som var så dype at kun han selv og brødrene hans kunne sitte i dem. De endte opp på Sankthansbålet for noen år siden… Antropometri er også viktig for kriminaletterforskerne. De kan for eksempel måle fotavtrykk på et åsted og bruke det til å anslå høyden på den personen de ettersøker. For en optimal lagervarebeholdning av ulike sko- og klesstørrelser i butikker trenger man også å vite noe om fordelingen av forholdene mellom ulike kroppsmål i befolkningen (hvor mange par damesko i størrelsene 36-40 skal butikken bestille?).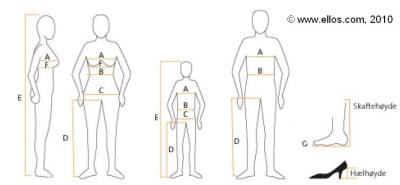
Matematikkstudenten Kristina Rognlien Dahl har i år hatt sommerjobb hos Norsk Regnesentral. Hun har bygd opp og analysert en database med fotlengden og kroppshøyden hos 250 personer. Hun har funnet én sammenheng mellom fotlengden og kroppshøyden til personer som har fotlengde over 25 cm, og en annen sammenheng for de med kortere fot. Likedan fant hun ut at det bør skilles mellom om man er over 13 år eller ikke. Barn vokser gjerne raskere enn voksne, og den tilpassede linja som beskriver sammenhengen er brattere for de unge. Analyser der vi finner den linja som best beskriver sammenhengen mellom for eksempel fotlengden og kroppshøyden kalles lineære regresjonsanalyser. Slike analyser brukes i mange sammenhenger. Et eksempel er arbeidene til de to kjente matematikerne Carl Friedrich Gauss (1777-1855) og Adrien-Marie Legendre (1752-1833). De gjorde lineæreregresjonsanalyser for å anslå banen til kometer basert på astronomiske observasjoner.
Norsk Regnesentral skal ha en stand på Forskningstorget 2010 i Oslo. Her vil alle kunne få målt sin fotlengde og høyde, og analysert måleresultatene sammen med andres. Man vil også kunne få sammenlignet sine egne mål med kjente personers. Vi har skuespiller Brad Pitt, sanger Rihanna, president Barack Obama og kunnskapsminister Kristin Halvorsen i databasen. Vi mangler bare deg!
Kom og besøk oss på Forskningstorget 2010! Les mer på forskningsdagene.no
| Ingunn Fride Tvete |
Jeg har vært ansatt på NR siden 2000. Jeg tok hovedfag i forsikringsmatematikk på Blindern i 2000, og doktorgrad i statistikk i 2006 på samme sted. Jeg har den siste tiden jobbet mest med helserelaterte problemstillinger, blant annet med analyser av reseptregisterdata og antibiotikaresistensproblematikken. Jeg driver også en del med metaanalyser, der man kombinerer resultater fra flere studier for å undersøke en eller flere sammenhenger. På fritiden min løper jeg mest, baker en del kaker, syr klær og quilter litt. |
Norge til fotball-EM?
september 10, 2010 - 15:20 — Magne AldrinNå er EM-kvalifiseringen i fotball godt i gang, og da klarer ikke vi å holde oss helt unna. Etter de første kampene har vi regnet oss fram til at Norge er favoritt i sin gruppe. Hvordan kan vi si det?
I utgangspunktet har en fotballkamp et element av både ferdighet og tilfeldighet. Et godt lag vil ofte slå et dårligere lag, men ikke alltid.
For å beskrive dette bruker vi en statistisk modell hvor hvert enkelt lag har et styrketall. Styrketallene til hvert lag tallfestes ut fra FIFA-rankingen, og av de fem lagene i Norges gruppe har i øyeblikket (8.9.2010) Portugal best FIFA-ranking, fulgt av Norge og Danmark. Norge er med andre ord et bedre lag enn Danmark ifølge FIFA-rankingen. Styrketallet til Portugal er fastsatt til 100. Vi tar også høyde for hjemmebanefordelen.
Styrketall per lag
|
Lag |
Styrketall |
|---|---|
|
Portugal |
100 |
|
Norge |
88 |
|
Danmark |
83 |
|
Kypros |
70 |
|
Island |
63 |
Et lite sidespor: Dette er litt forskjellig fra VM-beregningene våre, hvor vi (heldigvis) kom fram til at Spania lå best an før mesterskapet. I VM var det ingen hjemmebanefordel (bortsett fra for Sør-Afrika), og vi baserte oss på eksperttips istedenfor den noe omdiskuterte FIFA-rankingen.
Tilbake til EM: Etter at styrketallene er tallfestet, simulerer eller ”spiller” vi de resterende kampene i gruppa på en datamaskin. Deretter beregner vi tabellplasseringa til hvert enkelt. Tabellplasseringa bestemmes først av antall poeng, deretter av målforskjell, antall skårede mål og antall skårede mål på bortebane. Om to eller flere lag da står likt gjelder tilsvarende for innbyrdes oppgjør. Utfallet av hver kamp er tilfeldig, derfor blir det også i noe grad tilfeldig hvem som vinner gruppa i vårt simulerte gruppespill.
I virkeligheten spilles kampene kun én gang, men for å få fram det tilfeldige elementet gjentar vi vår øvelse 5 000 ganger. For hver gang registrerer vi H-U-B for hver enkelt kamp, og hvilket lag som kommer på de enkelte plassene til slutt. Ut fra dette beregner vi sannsynligheter for hvert enkelt lags muligheter. For eksempel beregnes sjansen for førsteplass ved å telle opp antall førsteplasser og dele på 5 000.
Vi har beregnet at Norges sjanser til å klare førsteplassen per i dag er 56 %, mens det er 26% sjanse for at Norge havner på andreplass (se tabellen). Hvis vi skjønnsmessig sier at det er 5/9=55% sjanse for å gå til EM med andreplass (fem av ni gruppetoere blir kvalifisert) gir det per i dag 70% sjanse for at Norge kvalifiserer seg til EM.
Sjanse for H-U-B per kamp
|
Hjemmelag |
Bortelag |
H (%) |
U (%) |
B (%) |
|---|---|---|---|---|
|
Kypros |
Norge |
29 |
26 |
45 |
|
Portugal |
Danmark |
54 |
24 |
21 |
|
Island |
Portugal |
18 |
23 |
58 |
|
Danmark |
Kypros |
53 |
24 |
22 |
|
Norge |
Danmark |
46 |
26 |
27 |
|
Kypros |
Island |
48 |
25 |
27 |
|
Portugal |
Norge |
50 |
24 |
25 |
|
Island |
Danmark |
27 |
26 |
47 |
|
Norge |
Island |
63 |
22 |
14 |
|
Kypros |
Portugal |
23 |
24 |
54 |
|
Island |
Kypros |
36 |
27 |
36 |
|
Danmark |
Norge |
38 |
27 |
35 |
|
Portugal |
Island |
70 |
19 |
11 |
|
Kypros |
Danmark |
31 |
27 |
42 |
|
Norge |
Kypros |
56 |
24 |
20 |
|
Danmark |
Portugal |
30 |
26 |
43 |
Plasseringsjanser per lag(%)
|
Lag/Plass |
1. |
2. |
3. |
4. |
5. |
|
Portugal |
17 |
32 |
30 |
17 |
4 |
|
Norge |
56 |
26 |
12 |
5 |
1 |
|
Danmark |
21 |
29 |
29 |
17 |
4 |
|
Kypros |
5 |
11 |
22 |
40 |
22 |
|
Island |
1 |
2 |
7 |
21 |
69 |
Med utgangspunkt i FIFA-rankinga er Portugal fortsatt ansett for å være det beste laget i gruppa, og er favoritt i alle sine resterende kamper. Men med sitt dårlige utgangspunkt er det mest sannsynlig at Portugal ikke klarer å ta igjen Norge.
Har dette noe med forskning å gjøre? Fotballberegningene er en lek med tall for å spre blest om faget. Men de illustrerer hvordan avanserte beregninger kan utføres, for eksempel ved estimering av fiskebestander eller sannsynligheten for at en bank går konkurs. I begge tilfeller er stokastisk simulering, altså å simulere virkeligheten på en datamaskin, et uvurderlig verktøy.
Beregningene ble oppdatert 8.9.2010, etter Norges hjemmekamp mot Portugal, og blogginnlegget er skrevet sammen med Anders Løland.




/index.jpg)
