sannsynlighet
Er nettpoker tilfeldig?
august 18, 2010 - 09:31 — Ragnar HaugePoker har kjempa hardt for å verta klassifisert som eit spel der ein vinn ved å vera dyktig, ikkje ved å ha flaks. Dette stemmer når ein ser det over mange nok spel, noko som viser seg ved at pokerspelande datamaskiner er i ferd med å verta uslåelege, akkurat som i sjakk. (http://manmachinepoker.com/)
Imidlertid er det framleis stor variasjon i utfallet over kortare periodar, slik som for ei enkelt turnering. Bridge, som også baserer seg på utdelte kort, har stabilisert dette ved at fleire spelar med same kortfordeling. Ein kan då sjå kven som gjorde det beste ut av korta, og utdelinga har dermed lite å seia. I poker er det vanskeleg å sjå for seg noko slikt.
Grunnlaget for å vera dyktig i poker er å vita kor sannsynleg ulike utfall er. Ut over det går spelet ut på å lesa dei andre spelarane, prøva å forutseia kva dei har ut frå kva dei gjer. For at ein skal kunne vita kor sannsynleg det er med dei ulike kombinasjonane, går ein ut frå at korta er rettferdig delt ut. I eit fysisk pokerlag kan ein uærlig delar øydeleggja dette ved å gi seg sjølv, eller meir subtilt ein medsamansvoren, systematisk betre kort.
Den store oppblomstringa av poker har imidlertid i det siste vore på nett, og då dukkar eit anna moment opp. For det første er det veldig vanskeleg å sjekka delinga, ein må stola på datamaskinen. For det andre har no delaren glede av at alle får litt betre kort.
Det mest sannsynlege utfallet i poker er å få ingenting, noko som ofte medfører at ein kastar seg. Det er ikkje så mange av hendene i eit vanleg pokerlag som verkeleg fører til skikkeleg satsing. Sidan pokerselskapa på nett tener pengar på å ta ein del av innsatsen, har dei glede av at det er meir satsing, altså at alle har betre kort. Eit anna moment er å halda på kundane, og mange vil føla at det er meir morosamt å spela ein stad der dei stadig får gode kort, sjølv om dei ikkje vinn så ofte som dei burde med desse. Tek ein dette endå lenger ser ein at nye kundar, eller kundar som har tapt ein del, bør kanskje få ekstra gode kort for å halda på dei.
Sjølv om skeivdelinga er systematisk og ikkje favoriserer nokon, vil den verka forstyrrande på gode pokerspelarar, som veit kva som er sannsynleg. Seriøse pokernettstadar legg derfor vekt på å overtyda kundane om at dei spelar rettferdig, hovudsakleg med to strategiar: Publisering av delingsalgortimane, og eksterne firma som PriceWaterhouseCoopers som validerer og går god for bruken av desse algoritmane.
Dette er ein god strategi, sjølv om den kan slå pinleg ut for den som ikkje har gjort jobben sin. I 1999 klarte ei gruppe dataekspertar å utnytta svake punkt i koden til ein pokernettstad, slik at dei fekk vita rekkjefølgja på korta i stokken, og dermed visste kva kort motstandarane hadde, og kva som ville koma av kort vidare. (http://www.cigital.com/papers/download/developer_gambling.php) Sidan det var snille gutar som gjorde dette, fortalde dei det til nettstaden, og venta til dei hadde ordna opp idet før dei gikk ut offentleg.
Når ein datamaskin skal sørgja for at noko vert tilfeldig, nyttar ein nesten alltid noko som vert kalla pseudotilfeldige tal. (Enkelte, som Norsk Tipping til Keno og Extra, nyttar ekte tilfeldige tal, men dette er for tregt for nettpoker.) Det finst algoritmar som gir sekvensar med tal som ser tilfeldige ut, men som er heilt systematiske. Dette er pseudotilfeldige tal. Dersom ein kjenner kva algoritme som vert nytta, og kva det forrige talet den gav var, veit ein kva det neste er.
Ekspertane kjente algoritmen for å generera tala, og korleis dette vart gjort om til ein stokka kortstokk, sidan dette var publisert. Det som mangla var å finna kvar i sekvensen av pseudotilfeldige tal ein var. Her var den store feilen i algoritmen: Nettstaden nytta klokkeslettet når spelet starta (koda på millisekundnivå) som startplass i sekvensen for delinga.
Ved å ha ein tilsvarande algoritme og søka gjennom kva resultat ein ville få ved å nytta initialtilstandar nær noverande klokkeslett, var det dermed berre å sjå kva tal som gav match med dei korta som var synlege. Med fem synlege kort var dette eintydig, og ein kjente dermed heile kortstokken.
Som nevnt over kjem ein neppe bort frå å nytta pseudotilfeldige tal i nettpoker, og det er viktig at algoritmen ein nyttar er offentleg kjent, slik at det ikkje er skjulte svake punkt. Det kritiske punktet er dermed å sørgja for at ingen kan gjetta kva initialisering som vert nytta ved delinga. Sidan initialisering kan gjerast sjeldnare (ein treng ikkje ein gong gjera det mellom kvar stokking, berre algoritmen er god nok) verkar det rimeleg at ein her nyttar ekte tilfeldige tal. I praksis nyttar dei seriøse aktørane fenomen som er nesten ekte tilfeldige, basert på mus- og tastaturbruk.
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |
Tålmodighetsprøven Lotto
august 11, 2010 - 11:35 — Anders Løland Her om dagen fikk jeg et spørsmål om Lotto:
Her om dagen fikk jeg et spørsmål om Lotto:
Øker vinnersjansen min hvis jeg ikke vant i forrige uke? Øker sjansen hvis jeg ikke har vunnet på ti år?
Spørsmålsstilleren vil nok være anonym, så jeg kaller ham Lotto-Lars. Lotto-Lars så for seg at sjansen øker hvis det er lenge siden forrige gevinst, siden det jevner seg ut i det lange løp. Det stemmer at det jevner seg ut i det lange løp, men dessverre for Lotto-Lars er vinnersjansen den samme hver uke og uavhengig av forrige ukes resultater: Hver uke begynner spillet på nytt.
Hvis Lotto-Lars ikke får noe igjen for at han ikke har vunnet på lenge, hvor lenge må han egentlig regne med å vente på den store gevinsten?
Sjansen for å vinne på en rekke i en Lotto-trekning er 1 av 5 379 616 (cirka 0,000 02 %). Lotto-Lars spiller 10 rekker i uka. Da må Lotto-Lars regne med å vente
537 961,6 uker
eller
10 345 år (hvis det er 52 uker i året) på sju rette!
Lotto-Lars kan være heldig og vinne allerede neste uke, men han kan også være uheldig og måtte vente lenge, lenge. Spesielt fortærende er det nok at han ikke får igjen for å ikke å ha vunnet tidligere.
Kanskje hjelper det litt med trøstepremien (4 rette + 1 tilleggstall), hvor vinnersannsynligheten er omtrent 0,6 %. Den vil Lotto-Lars i gjennomsnitt vinne hver 17. uke.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
Hva skjedde med Spania?
juni 22, 2010 - 11:55 — Anders LølandFør VM regnet NR ut at Spania hadde 21% sjanse for å vinne fotball-VM. Etter at alle gruppene har gjennomført to av tre runder, har det skjedd mye.
La oss gå rett på sak. Figuren under viser sannsynligheten for 1. plass for de tolv nåværende favorittene per i dag, etter kampene spilt 21. juni, samt utviklingen i vinnersannsynlighetene siden VM startet.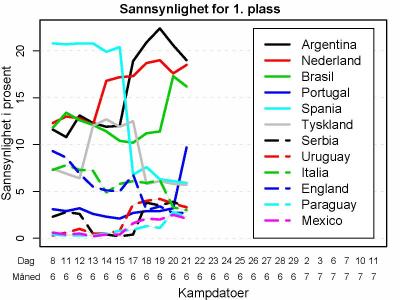
Mens Spania var favoritten og har rotet det til, er nå Argentina, Nederland og Brasil de tre klart største favorittene til å vinne VM. Sannsynligheten er nå over 50% prosent for at et av disse tre landene stikker av med pokalen. Dette er en konsekvens av kampene som er spilt så langt.
Det var noe skepsis til Argentina før VM, men etter to klare seire har de klatret til topps så langt.
Tyskland startet med en vinnersjanse på 7,5%. Den økte til rundt 12% etter den første seieren mot Australia, men falt igjen etter tapet mot Serbia.
Bakfra kommer Uruguay, Paraguay og Mexico, som har styrket sine sjanser betraktelig etter forhåndstipset på cirka 0,5%.
Beregningene er basert på at hvert lag tilordnes et styrketall før hver kamp. Ut fra styrketallene til to lag som møtes, skal en kunne avlese sannsynligheten for seier, uavgjort og tap. Styrketallene vil være noe à la FIFA-rankingen, men mer direkte relatert til utfallet av enkeltkamper.
Argentina, Nederland og Brasil har nå omtrent samme styrketall. Det betyr at NR-modellen mener de nå er omtrent like gode lag. Tilsvarende har Spania litt høyere styrketall enn Portugal, men lavere sannsynlighet for å vinne (9,5% mot 6%), siden Portugal i praksis er klare for åttendelsfinalen, mens Spania må vinne kampen mot Chile.
Modellen var før VM basert på tipsene til 14 fotballeksperter fra TV 2 Sporten. Eksperttipsene og de virkelige kampene blir vektet i forhold til hverandre, slik at eksperttipsene har like stor betydning som de virkelige kampene etter at hvert lag har spilt to kamper. Når alle lag har spilt flere enn to kamper betyr derimot de virkelige kampene mest.
Sannsynlighetene oppdateres hver dag under hele VM basert på kampene som blir spilt, og her kan det som vi har sett endre seg fort. Følg med videre på vm.nr.no!
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
For få frisparkmål i VM?
juni 21, 2010 - 11:53 — Anders LølandTil tross for 53 forsøk, har det hittil i VM ikke blitt scoret mål på direkte frispark. Skyldes dette JABULANI, den mye omtalte ballen, eller er det bare tilfeldighetene som er ute og går?
Ifølge en dokumentar sendt på britiske ITV har det i gjennomsnitt blitt mål på hvert 20. frispark i tidligere fotball-VM. Derfor burde vi sett minst to frisparkmål allerede. Men så har vi disse tilfeldighetene da.
Hvis vi går litt vitenskapelig til verks kan vi sette opp følgende påstand:
Det blir i gjennomsnitt mål på hvert 20. frispark.
Det betyr at sannsynligheten for mål er 5% per frispark. Vi antar her at hvert frispark er uavhengig av alle andre frispark.
Siden jeg som statistiker ikke kan fri meg fra å tro at dette kan skyldes tilfeldigheter, vil jeg ikke gi slipp på at hvert 20. frispark gir mål før sannsynligheten for at det er tilfeldig er under 5%, noe den ikke er ennå.
Først etter 59 frispark uten mål kan vi si at dette ikke er tilfeldig, og at det scores uvanlig få frisparkmål i årets VM. Det kan med andre ord skyldes tilfeldigheter, men er helt på grensen.
Det kan komme av JABULANI, men det finnes selvfølgelig andre muligheter. For eksempel kan det være de fæle VUVUZELAene som gjør frisparkerne mo i knærne!
For de spesielt interesserte kan jeg røpe at hvis jeg er strengere, og krever at sannsynligheten for at manglende frisparkmål skyldes tilfeldigheter er under 1%, er det først etter 91 frispark uten frisparkmål jeg med god samvittighet kan skylde på JABULANI eller noe annet.
Dette innlegget ble skrevet rett etter Italias trasige 1-1-kamp mot New Zealand på søndag. Følg med på http://vm.nr.no/ for oppdaterte sannsynligheter for de ulike lagenes plasseringer.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
Måtte det beste laget vinna?
juni 11, 2010 - 10:24 — Ragnar HaugeEin rein cup er lite eigna til å kåra det beste laget i ei gruppe, spesielt i idrettar der utfallet av enkeltkampar kan vera ganske tilfeldig. Fotball er eit godt eksempel her - kampar vert ofte avgjort med berre eitt mål, og då kan det fort vera tilfeldig kven som får det målet. Det er neppe grunn til å tru at Fyllingen er eit betre lag enn Brann, det same gjeld Tønsberg vs Vålerenga, men det er likevel Fyllingen og Tønsberg som framleis kan vinna NM i fotball.
Når ein er ute etter å kåra den beste på meir sikkert grunnlag er det derfor mest vanleg å nytta eit seriesystem. Med så mange kampar som det involverer, vil flaksen jamna seg ut etter kvart - og eit lag kan ikkje verta eliminert frå konkurransen med uflaks i ein enkelt kamp.
I eit seriesystem taper ein likevel duellaspektet, det fascinerande med at ein part må vinna, ein må tapa. Kvar kamp vert på sett og vis mindre viktig. I ein del idrettar vert det derfor nytta eit utvida cupsystem, der laga framleis møtest og slår kvarandre ut parvis, men i staden for at dette skjer på grunnlag av ein enkelt kamp, vert det spela fleire kampar, og vinnaren er den som vinn flest av desse. Typisk er det til dømes tenkt 7 kampar, så vinnaren er den første som vinn 4 (eventuelt uspela kampar vert då ikkje spela, sidan det allereie er klart kven som vinn flest).
Best av tre vert ikkje nytta eksplisitt i nokon stor idrett, men ligg innebygd i ein del settbaserte idrettar, som tennis og strandvolleyball. Det er likevel berre snakk om ein kamp. Best av fem finn ein og innebygd i tennis, men den vert også nytta i sluttspelet i baseball i USA. Dette sluttspelet vert spela som ein cup, og i første runde av denne er det best av 5 som gjeld, før ein går over til best av 7. Dette finn ein i dei fleste store amerikanske idrettane, og norsk ishockey har også adoptert dette for sin cup. Historisk har det også vore brukt best av 9, men dette er ikkje i bruk i nokon større idrett no.
Kva har så dette å seia for utfallet? Eg går ut frå at kvar kamp vert avgjort (sudden death, straffekonkurranse e.l.). I eit møte mellom to lag der det eine vinn dobbelt så ofte som det andre vil det dårlegaste laget likevel vinna 1/3 av gongane dersom berre ein enkelt kamp tel. Dersom ein spelar best av 3 går dette ned til 26% av gongane, best av 5 gir 21%, og best av 7 er nede på 17%, halvparten av sjansen med berre ein kamp.
 Dersom laga er jamnare, med 60% sjanse for det eine og 40% for det andre i kvar kamp, vert dette endra til 65% og 35% i best av 3. I best av 5 har det dårlegaste laget 32% sjanse til å vinna, og med best av 7 er denne nede på 29%. Når laga er jamnare gjer det altså mindre utslag å spela mange kampar.
Dersom laga er jamnare, med 60% sjanse for det eine og 40% for det andre i kvar kamp, vert dette endra til 65% og 35% i best av 3. I best av 5 har det dårlegaste laget 32% sjanse til å vinna, og med best av 7 er denne nede på 29%. Når laga er jamnare gjer det altså mindre utslag å spela mange kampar.
Hovudargumentet for berre ein kamp er likevel å ha ein avgjerande kamp, den viktige kampen. Kamp 2 i ein finale over 7 kampar har ikkje same trykk som den eine finalekampen der alt skal avgjerast. I tillegg har det sin sjarm at den beste kan tapa. Så i VM gir også ishockey slepp på sine multiple kampar, og spelar enkeltkampar med vinn eller forsvinn dei tre siste rundane. Noko Tsjekkia kanskje hadde glede av i år?
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |



