Hva skjedde med Spania?
Før VM regnet NR ut at Spania hadde 21% sjanse for å vinne fotball-VM. Etter at alle gruppene har gjennomført to av tre runder, har det skjedd mye.
La oss gå rett på sak. Figuren under viser sannsynligheten for 1. plass for de tolv nåværende favorittene per i dag, etter kampene spilt 21. juni, samt utviklingen i vinnersannsynlighetene siden VM startet.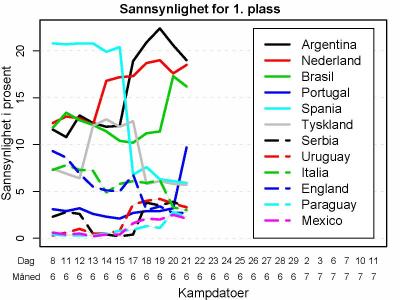
Mens Spania var favoritten og har rotet det til, er nå Argentina, Nederland og Brasil de tre klart største favorittene til å vinne VM. Sannsynligheten er nå over 50% prosent for at et av disse tre landene stikker av med pokalen. Dette er en konsekvens av kampene som er spilt så langt.
Det var noe skepsis til Argentina før VM, men etter to klare seire har de klatret til topps så langt.
Tyskland startet med en vinnersjanse på 7,5%. Den økte til rundt 12% etter den første seieren mot Australia, men falt igjen etter tapet mot Serbia.
Bakfra kommer Uruguay, Paraguay og Mexico, som har styrket sine sjanser betraktelig etter forhåndstipset på cirka 0,5%.
Beregningene er basert på at hvert lag tilordnes et styrketall før hver kamp. Ut fra styrketallene til to lag som møtes, skal en kunne avlese sannsynligheten for seier, uavgjort og tap. Styrketallene vil være noe à la FIFA-rankingen, men mer direkte relatert til utfallet av enkeltkamper.
Argentina, Nederland og Brasil har nå omtrent samme styrketall. Det betyr at NR-modellen mener de nå er omtrent like gode lag. Tilsvarende har Spania litt høyere styrketall enn Portugal, men lavere sannsynlighet for å vinne (9,5% mot 6%), siden Portugal i praksis er klare for åttendelsfinalen, mens Spania må vinne kampen mot Chile.
Modellen var før VM basert på tipsene til 14 fotballeksperter fra TV 2 Sporten. Eksperttipsene og de virkelige kampene blir vektet i forhold til hverandre, slik at eksperttipsene har like stor betydning som de virkelige kampene etter at hvert lag har spilt to kamper. Når alle lag har spilt flere enn to kamper betyr derimot de virkelige kampene mest.
Sannsynlighetene oppdateres hver dag under hele VM basert på kampene som blir spilt, og her kan det som vi har sett endre seg fort. Følg med videre på vm.nr.no!
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |



Modellen
Et spørsmål:
Etter de virkelige kampene er spilt så oppdaterer dere styrketallet basert på resultatene.
Men i simulasjonene kan dere også gjøre det. Gjør dere det?
Altså 2 alternativer:
1. Før simulasjonen starter er styrketall fastsatt som normalt. Uavhengig av de første resultatene
i en gitt simulasjon, simulerer dere resten av kampene med samme styrketall som dere startet med.
2. Før simulasjonen starter er styrketall fastsatt som normalt. Etter hver simulerte kamp i en gitt simulasjon,
så oppdaterer dere styrketallene basert på den simulerte kampen. Og disse oppdaterte styrketallene benyttes for
resten av DENNE simulasjonen.
Modellen
Takk for spørsmålet.
Vi bruker alternativ 1. Gitt oppdaterte styrketall, trekker (eller simulerer) vi første kamp, neste kamp, og så videre. I noen trekninger vinner favoritten(e), i andre ikke, men gjennomsnittet av trekningene gjenspeiler styrkeforholdene mellom lagene. Alternativ 2 er ikke noen dårlig idé, men krever mer beregningstid.
Modellen
Alternativ 2 er en dårlig ide fordi den gir eksakt samme resultat som alternativ 1, i det minste i en Bayesiansk setting. Eksempel: Anta at prior på parameterne er
f(theta),
at x1 gitt theta har fordeling
f(x1|theta)
og at x2 gitt x1 og theta har fordeling
f(x2|x1,theta).
Alternativ 1 innebærer da å først simulere theta fra prior, så x1 gitt theta, og så x2 gitt x1 og theta. Da vil x2 få rett fordeling, d.v.s.
f(x2) = int int f(x2|x1,theta) f(x1|theta) f(theta) dtheta dx1.
Alternativ 2 innebærer at vi skal simulere x2 ved å simulere fra fra f(x2|x1,theta) men med theta valgt fra oppdatert fordeling til theta etter at vi har fått kjennskap til x1,
f(theta|x1) = f(x1|theta)f(theta)/f(x1) (Bayes teorem)
Gjør vi dette blir fordelingen til x2
int f(x2|x1,theta) f(theta|x1) dtheta
= int f(x2|x1,theta) f(x1|theta) f(theta) / f(x1) dtheta
= int f(x2|x1,theta) f(x1|theta) f(theta) dtheta / f(x1)
= int f(x2,x1,theta) dtheta / f(x1)
= f(x1,x2) / f(x1) = f(x2),
m.a.o. rett fordeling og eksakt det samme som for alternativ 1.