Kan statistikere spille Lotto?
For en tid tilbake raljerte jeg over hvor håpløst det er å spille Lotto. Til tross for det, spiller jeg av og til.
Min bortforklaring kommer her: En ukentlig innsats på 20 kroner er så lite at jeg ser bort fra den. (I tillegg går jo Norsk Tippings overskudd til en god sak.) Å vinne førstepremien, derimot, hadde unektelig vært ganske kjekt. Så til tross for at Lotto nesten helt sikkert er et tapsprosjekt, ser jeg bort fra tapet og fokuserer ensidig på den mulige gevinsten.
For å vitenskapligfisere dette enda litt mer, har jeg laget min egen nyttefunksjon. En nyttefunksjon tallfester en aktørs nytte av noe. I mitt tilfelle har jeg null nytte av Lotto-innsatsen i seg selv, mens jeg har en temmelig positiv nytte av en høy gevinst.
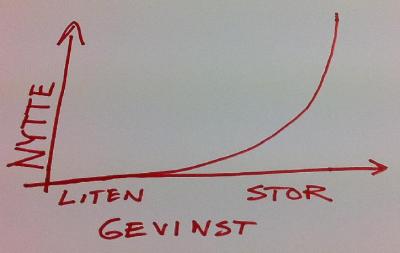
Dersom jeg hadde vært litt mer rasjonell, ville min forventning vært negativ:
forventet gevinst = –innsats + sannsynlighet for gevinst x gevinst < 0.
Med min nyttefunksjon får jeg en positiv forventet nytte:
forventet nytte = –nytte av innsats + sannsynlighet for gevinst x nytte av gevinst
= 0 + sannsynlighet for gevinst x nytte av gevinst > 0,
siden jeg ser bort fra innsatsen.
Nyttefunksjoner brukes ofte i økonomisk teori, for eksempel til å regne på og forklare hvilke valg vi (rasjonelle?) forbrukere gjør.
Nyttefunksjonens slektning brukes også i statistisk-matematisk modellering. Da kalles de slående nok tapsfunksjoner. Her vil en typisk at en modell skal være så god som mulig, med andre ord minimere tapsfunksjonen.
Det er ikke alltid åpenbart hvilken tapsfunksjon en skal velge. Dette henger igjen sammen med det såkalte "Ockhams barberkniv"-prinsippet: Med to mulige, men like gode, forklaringer, er det mest sannsynlig at den enkleste er best.
I mitt tilfelle er det uansett klart at min Lotto-nyttefunksjon er en funksjon som med høy sannsynlighet garanterer tap.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |



Underholdning
Jeg tipper og kjøper lodd svært sjeldent. Men når jeg gjør det forsvarer jeg det på en helt annen måte:
1. Jeg kjøper meg underholdning og spenning
2. Jeg støtter en god sak (i de tilfelle der det er gjeldende)
Forøvrig sier ikke Ockhams razor direkte at man skal velge den enkleste løsningen. Det den sier er omtrent at dersom to forklaring inneholder de samme elementene, men den ene inneholder noen ekstra som den andre ikke har, så velg bort alternativet med overflødige elementer.
Den tradisjonelle bruken er i forhold til Gud og skapelsen av universet. Kan man postulere en uendelig eksistens som inneholder en Gud som er opphavet til vårt univers, så kan man også postulere en uendelig eksistens uten Gud som er opphavet til vårt univers. Å legge til elementet Gud gir ikke bedre forklaringskraft, og er derfor unødvendig.
Lotto
Interessant poeng, men likevel er det litt vel irrasjonelt. Det er greit at man kan konstruere en "unnskyldning" for seg selv ved å si at man simpelthen ser bort fra de 20 kronene. Problemet er imidlertid at penger er penger uansett hvor stort beløpet er og alle har et begrenset budsjett. Hver eneste krone har alternativ bruk. Rentesrenteeffekten er over tid meget sterk, noe som fører til at tilsynelatende ubetydelige beløp kan bli store.
Hvis målet ditt er muligheten for å sitte igjen med en god sum med penger om f.eks. 40 år og man helt ser bort fra 20 kr i uken, finnes det måter å stue pengene bort på som med stor grad av sannsynlighet (i motsetning til med Lotto) gir deg mye penger ved utløpet av 40 år.
Eksempel: Du er 20 år i dag og setter av 20 kr hver uke. Ved slutten av første året har du satt av 1040 kr. Bare ila. et år har de ubetydelige pengene blitt nok til et digitalkamera. Du setter imidlertid heller pengene inn i et billig aksjeindeksfond som over tid er forventet å gi deg 10% årlig avkastning etter kostnader. Neste år har du spart opp nye 1040 kr i tillegg til at de opprinnelige har vokst med 10% til 1144 kr = 2184. Dette gjentar du hvert år frem til du nærmer deg pensjonsalder som 60-åring. På slutten av 40-årsperioden har pengene du ikke merket hver uke vokst til 460.296 kr. Over en 40-årsperiode er det relativt sannsynlig at du vil sitte igjen med ca. dette beløpet ettersom svinginger i aksjemarkedet har en tendens til å utjevne seg over tid. I Lotto er det relativt sannsynlig at du har tapt flere titalls tusen, altså en differanse på ca. 0,5 mill. Ved å ofre litt av Lotto-spenningen hver uke, kan du gi deg selv en ny, bra bil i 60-årsgave. Legg merke til at her investerer man bare ved slutten av hvert år og ikke f.eks. hver måned. Renter/avkastning på pengene i spareperioden er ikke regnet med. Det betyr at avkastningen reelt sett ville blitt høyere.
Skulle du ha flaks og heller velge et aktivt fond som klarer 15 % i året, sitter du igjen med 1,85 mill om 40 år, altså ca. 1,4 mill mer enn ved 10% avkastning. Altså ca. en Lottogevinst i differanse. Det er usannsynlig at du klarer å finne en forvalter som er så god, men likevel langt mer sannsynlig enn å vinne 1. premie i Lotto...
Konklusjon: Selv med en nyttefunksjon der man ser bort fra små beløp hver uke og verdsetter muligheten for et høyt sluttbeløp høyt, er det bedre å være rasjonell og investere pengene fornuftig enn å spille Lotto.