Blogger
Luftforurensning, trafikk og litt salt
mars 16, 2011 - 14:28 — Gunnhildur Høgnad...Går du langs en trafikkert vei en vakker og kald vinterdag, er du antakeligvis ikke tvil om at flere biler gir mer forurensning. Det er velkjent at luftkvaliteten blir dårligere på ekstra kalde og solrike vinterdager hvor luften blir liggende som et stillestående lokk over byen. Hva er så poenget med å lage modeller som bekrefter sammenhenger du kanskje allerede visste om?

Luftkvalitet langs veien
For å få bedre kunnskap om luftkvaliteten langs veiene, har NR i et samarbeid med Statens Vegvesen sett på sammenhengen mellom trafikkrelatert forurensning og andre komponenter som påvirker lufta, som for eksempel meteorologi. Med statistiske modeller kan vi kanskje oppdage sammenhenger som vi ikke var klar over. Et annet viktig poeng er at en statistisk analyse kan kvantifisere effekter og sammenligne ulike luftforurensningskomponenter på en systematisk måte.
I denne analysen brukte vi målinger av konsentrasjonen av ulike forurensningsgasser og svevestøvpartikler fra en målestasjon langs Kirkeveien i Oslo. Både gassene og svevestøvpartiklene kan utgjøre en helseskade for mennesker og en risiko for miljøet. Luftkvalitetsmålingene hadde timesoppløsning fra 2001 til 2009, det vil si en periode som tilsvarer over 70000 timer. (Alle statistikere blir glade når de får mye data, gitt at kvaliteten på dataene er god nok.) I tillegg brukte vi meteorologiske data (vindstyrke, vindretning, temperatur, nedbør, snødybde og relativ fuktighet), trafikkvolum, gjennomsnittshastighet på trafikken samt bladvegetasjons- og piggdekkandel.
Salt mot veistøv
Statens Vegvesen bruker en saltløsning med magnesiumklorid på veiene for å dempe svevestøvkonsentrasjonen. Magnesiumklorid holder veibanen fuktig noe som kan bidra til at svevestøvet holder seg på veien og ikke virvles opp i lufta. I perioden 2005 til 2009 ble det gjennomført i snitt 15 tiltak med magnesiumklorid hver vintersesong. Hensikten med tiltakene er å redusere konsentrasjonen av svevestøv på dager med ekstremt mye forurensning. Tiltakene er altså ikke det samme som ordinær vinterdrift hvor salt brukes på snø og is.
For å kvantifisere effekten av støvdempingstiltakene, må vi korrigere for andre faktorer som påvirker luftkvaliteten. Vi må altså kunne vite om det er saltingen eller om det er for eksempel en gunstig vindretning eller nedbør som bedrer luftkvaliteten. Med andre ord, vi bruker vår statistiske modell og korrigerer for alle andre effekter slik at vi kun står igjen med effekten av saltetiltaket.
Vi fant, vi fant
Hvilke spennende funn finner vi ved en slik analyse? Noen resultater er opplagte, som at luftforurensning økte med økende antall lette kjøretøyer. Kanskje ikke fullt så opplagt er at en økning fra ingen til noen få biler utgjorde en stor forskjell på luftkvaliteten. Andre eksempler på resultater er at konsentrasjonen av PM2,5 (små partikler mindre enn 2,5 mikrometer) og gassen CO ble lite påvirket av tungtrafikken. Vindretningen og måleapparatets plassering i forhold til veien, hadde også mye å si, spesielt for gassene. Den dominerende vindretningen med mest forurensning var når det blåste langs med veien, mens det var mindre forurensning hvis vinden blåste fra måleapparatet og vinkelrett på veien.
Og hjelper det så å støvdempe med salt? Analysen vår viste at konsentrasjonen av PM10 (partikler som er mindre enn 10 mikrometer) ble redusert med 14 % umiddelbart etter et tiltak, men det hadde ingen effekt på de mindre PM2,5. Størst effekt fant vi på differansen PM10-PM2,5 (partikler mellom 2,5 og 10 mikrometer) med en reduksjon på 27 %. Det er viktig å poengtere at denne analysen ikke har tatt for seg de negative sidene ved å bruke salt, som skader på miljøet og rustødeleggelser på biler. Dessuten har vi kun undersøkt luftforurensning rett ved veien og ikke sett på effekter lenger unna målestasjonen.
Så hvis du fortsatt går langs en trafikkert vei en vakker vinterdag, kan du håpe at det er litt vind og at vinden blåser riktig vei i forhold til deg. Eller du kan håpe at flere gjør som deg, nemlig lar bilen stå.
| Gunnhildur Høgnadottir Steinbakk |
Jeg har jobbet som forsker på NR siden år 2000. Jeg har min utdannelse fra Universitetet i Oslo, med hovedfag i anvendt og industriell matematikk og doktorgrad i statistikk. På NR har jeg jobbet med ulike statistiske anvendelser, spesielt problemstillinger knyttet til miljø og marin. For øyeblikket bruker jeg mye av fritiden på mine to barn og på å pusse opp vårt 1700-talls torp i Sverige. Ellers liker jeg å være sammen med venner, spise god mat, sykle, gå tur og spille innebandy. |
Å gjenskape storskalamønstre
februar 18, 2011 - 17:27 — Heidi KjønsbergFor best mulig håndtering av olje- og gass-reservoarer er det i petroleumsbransjen vanlig å lage matematiske modeller av reservoarene. Ved slik modellering defineres ofte et 3D-gitter, og så tenker en seg at gitter-cellene fylles med forskjellige steintyper som sand og skifer. Mønstrene som da lages av den oljeholdige sanda og den ugjennomtrengelige skiferen bestemmer om og hvordan oljen/gassen kan flyte i reservoaret. Siden mye er ukjent om virkelige reservoarer er det nødvendig å bygge inn usikkerhet i modellene, og studere sannsynlighetene for de forskjellige flytegenskapene.
Markov mesh modeller er en metode for å fylle gitter-cellene på en fornuftig måte, og samtidig håndtere disse usikkerhetene. En starter med et tredimensjonalt “treningsbilde”, og lager så en matematisk modell som analyserer og lagrer de forskjellige treningsbildemønstrene. Denne modellen brukes så for å simulere nye tredimensjonale gitter, som hver seg likner på treningsbildet, men som samlet spenner ut det som finnes av mønstermuligheter/usikkerhet. I tillegg til treningsbildeinformasjonen kan en betinge på seismiske data og brønndata under simuleringen. Da reduserer usikkerhetene.
En komplikasjon oppstår dersom treningsbildet har mønstre på mye større skala enn gitteret selv. Siden Markov mesh modellen bare bruker informasjon fra et begrenset område rundt hver gittercelle under simuleringen av steintyper, kan den ikke “se” langt nok til å fange opp disse storskalamønstrene.
Dette problemet har vi på NR løst ved å bruke mange påfølgende gitter-forfininger. Først simulerer vi celler på et svært grovt gitter, deretter forfiner vi det tredimensjonale gitteret i én retning om gangen, og for hver forfining simulerer vi de nye cellene. Til slutt har vi forfinet så mye i hver retning at vi har kommet ned til det fineste gitteret, og simuleringen er ferdig.

Metoden med multiple gitter benyttes også av andre multipunkts-metoder. Men ved å bruke den i Markov mesh modelller oppnår vi å kombinere den smarte gitter-bruken med en metode som er matematisk konsistent og gir raske simuleringer. Resultatene er fine og viser at metoden har god evne til å håndtere mange forskjellige typer treningsbilder. Det gjør den anvendelig i mange geologiske settinger, og hjelper oljeselskapene til å få god kontroll på reservoarmodellene de bruker for å planlegge og drifte utvinning av olje og gass.
| Heidi Kjønsberg |
Jeg har jobbet på NR siden 2005, og er seniorforsker i avdelinga for Statistical Analysis of Natural Resource Data. Utdanninga mi har jeg fra Universitetet i Oslo, med en doktorgrad i teoretisk fysikk fra 1998. Jeg har jobbet med kvantefysikk, som forsker i telecom-industrien, og siden jeg startet på NR med matematisk modellering av olje- og gassreservoarer. På fritida lager jeg ofte mye og ganske god mat. Men gjester må finne seg i eksperimentering og tildels mye chili. Jeg liker fysisk arbeid, og holder på å lære meg å gjenkjenne fuglearter fra lyd og utseende. |
Kristen Nygaards hus
februar 11, 2011 - 12:12 — Lars HoldenJulen 2010 flyttet Institutt for Informatikk ved Universitetet i Oslo inn i det nye Ole Johan Dahls hus. Det er derfor naturlig at (den første) Informatikkbygningen skifter navn. Det var aldri tvil om at bygningen skulle oppkalles etter Kristen Nygaard. Jeg benytter anledningen til å gi en kort beskrivelse av Kristen Nygaard.

Avhengig av bakgrunn vil de fleste enten kjenne ham som en av oppfinnerne av Simula, det første objektorienterte programmeringsspråket, eller lederen av “Nei til EU” fra 1990 til 1995. Dette viser bare noe av spennvidden i Nygaards engasjement.
Nygaard var en mann med et stort talent, brennende engasjement og bredt interessefelt. Hans talent viste seg tidlig, og han viste akademiske interesser alt tidlig i tenårene. Mens han gikk på gymnaset fulgte han universitetsstudier og vant en matematikkpris. Hvis et tema først fanget hans interesse, slukte han alt stoff om området og erklærte seg som ekspert. Områdene inkluderte alt fra klassisk musikk til fotografering og vin i senere år. I en rekonvalesensperiode i 1962-63 måtte han ta det med ro. Han brukte tiden til å lese Carl Grimbergs 22-binds verdenshistorie, og han kunne gjengi detaljer herfra resten av sitt liv. Han dominerte enhver gruppe og var ofte en naturlig leder, blant annet fordi han selv var umulig å lede.
Han arbeidet med operasjonsanalyse ved Forsvarets forskningsinstitutt (FFI) fra 1948 til 1960. En problemstilling kunne for eksempel være “hvor langt kan en soldat gå i tungt terreng med stor oppakning?” For Nygaard var det naturlig selv å delta i eksperimentene. Den samme tilnærmingen hadde han innen alle områder han arbeidet. Han ville selv være en aktiv bruker og testet ut utstyr og dataprogrammer. Han kunne bruke mye tid på å diskutere de minste detaljer i funksjonaliteten.
Da Nygaard begynte på Norsk Regnesentral (NR) i 1960 var målsetningen å bygge en sivil operasjonsanalysegruppe. De fleste fra operasjonsanalysegruppen ved FFI fulgte ham, blant annet Ole-Johan Dahl. I 1962 klarte Nygaard å få en av Europas kraftigste datamaskiner til NR. I løpet av de neste årene ble Simula, verdens første objektorienterte programmeringsspråk, utviklet. Nygaard hadde mange av de store vyene, mens Ole-Johan Dahl så hvordan de kunne implementeres. I dag bygger de fleste programmeringsspråk på disse prinsippene.

Da Nygaard begynte å arbeide ved Institutt for informatikk ved Universitetet i Oslo i 1984, var hovedaktiviteten systemarbeid. Han fortsatte imidlertid også arbeidet med objektorientering ved å utvikle nye programmeringsspråk. Etter at han ble pensjonist ble han igjen ansatt ved NR, men nå i deltidsstilling. Han startet opp et prosjekt om hvordan objektorientering skulle undervises og arbeidet med dette frem til han døde.
Nygaard var politisk engasjert fra han var ung, først som aktiv i Venstre, og i Arbeiderpartiet fra slutten av 60-årene. Hans viktigste politiske verv var imidlertid oppbyggingen av “Nei til EU”, som ledet fra 1990 til 1995. Dette var en meget bred politisk bevegelse som han samlet ved bruk av sin brede kunnskap, politisk kløkt og taktisk spill. Bevegelsen medvirket til at Norge ikke ble medlem av EU etter en folkeavstemming i 1994.
Hans politiske kontakter førte til at han på slutten av 60-tallet underviste om moderne teknologi på LO-skolen. Dette banet veien for flere forskningsprosjekter om innføring av EDB, og senere til verdens første avtale mellom partene i arbeidslivet om innføring av EDB på en arbeidsplass. Det skjedde i 1974. Det har vært hevdet at dette arbeidet har bidratt til at innføring av EDB har gitt færre konflikter i Norge enn i mange andre land. På lik linje med Simula var dette nybrottsarbeid. Nygaard introduserte bidrag fra fagforeninger i forskningsprosjekter og mente at resultatene burde påvirke tariffavtalene.
I alt arbeid utviste Nygaard stort engasjement og var ofte overstrømmende i møte med mennesker, men som oftest mer tilstedeværende i initiativet og oppstarten enn i gjennomføringen og rapporteringen. Å følge opp tidligere forpliktelser var ikke hans sterkeste side. Nygaard viste også stort internasjonalt engasjement og ble anerkjent for dette i mange land. Nygaard fikk Norbert-Wienerprisen for sitt sosiale engasjement innen databehandling, som den første ikke-amerikaner i 1990.
Sammen med Ole-Johan Dahl ble han kommandør av Sankt Olavs Orden i 2000. De to vant Turing-prisen i 2001 og von Neumann-medaljen i 2002, de fremste prisene innen IKT.
Kristin Nygaard var kontroversiell og gikk ofte inn i konflikter med stor tyngde og glede. I en tale til NTNF, en forløper til forskningsrådet, sa han: “Det er deres penger, men det er våre liv.” Han la heller ikke skjul på at han var kontroversiell og sa: “Har noen kritisert ditt arbeid i det siste? Hvis ikke, hva er din unnskyldning?“
Han døde i 2002, 75 år gammel, og hadde sterke meninger og var en aktiv forsker til det siste.
| Lars Holden |
Jeg ble ansatt på Norsk Regnesentral i 1984 og har vært adm. dir. siden 2001. Jeg har flere styreverv, bl.a. er jeg styreleder i Forskningsinstituttenes fellesarena, i Samarbeidsutvalget mellom UoH-sektoren og instituttsektoren og i forskning.no. Det gjør at jeg bruker det meste av tiden på ledelse og forskningspolitikk. Jeg var i en periode professor II i anvendt matematikk og er fortsatt en aktiv forsker innen anvendt matematikk og statistikk. De siste årene har forskningen dreid seg mest om anvendelser innen medisin og økonomi, men jeg er også interessert i andre anvendelsesområder. Det meste av fritiden bruker jeg på trening og familien. |
Kan statistikere spille Lotto?
november 9, 2010 - 09:48 — Anders LølandFor en tid tilbake raljerte jeg over hvor håpløst det er å spille Lotto. Til tross for det, spiller jeg av og til.
Min bortforklaring kommer her: En ukentlig innsats på 20 kroner er så lite at jeg ser bort fra den. (I tillegg går jo Norsk Tippings overskudd til en god sak.) Å vinne førstepremien, derimot, hadde unektelig vært ganske kjekt. Så til tross for at Lotto nesten helt sikkert er et tapsprosjekt, ser jeg bort fra tapet og fokuserer ensidig på den mulige gevinsten.
For å vitenskapligfisere dette enda litt mer, har jeg laget min egen nyttefunksjon. En nyttefunksjon tallfester en aktørs nytte av noe. I mitt tilfelle har jeg null nytte av Lotto-innsatsen i seg selv, mens jeg har en temmelig positiv nytte av en høy gevinst.
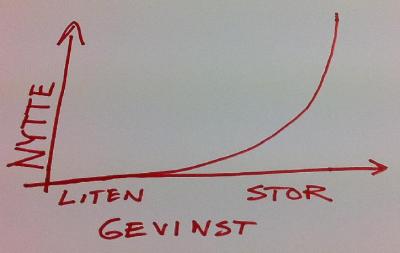
Dersom jeg hadde vært litt mer rasjonell, ville min forventning vært negativ:
forventet gevinst = –innsats + sannsynlighet for gevinst x gevinst < 0.
Med min nyttefunksjon får jeg en positiv forventet nytte:
forventet nytte = –nytte av innsats + sannsynlighet for gevinst x nytte av gevinst
= 0 + sannsynlighet for gevinst x nytte av gevinst > 0,
siden jeg ser bort fra innsatsen.
Nyttefunksjoner brukes ofte i økonomisk teori, for eksempel til å regne på og forklare hvilke valg vi (rasjonelle?) forbrukere gjør.
Nyttefunksjonens slektning brukes også i statistisk-matematisk modellering. Da kalles de slående nok tapsfunksjoner. Her vil en typisk at en modell skal være så god som mulig, med andre ord minimere tapsfunksjonen.
Det er ikke alltid åpenbart hvilken tapsfunksjon en skal velge. Dette henger igjen sammen med det såkalte "Ockhams barberkniv"-prinsippet: Med to mulige, men like gode, forklaringer, er det mest sannsynlig at den enkleste er best.
I mitt tilfelle er det uansett klart at min Lotto-nyttefunksjon er en funksjon som med høy sannsynlighet garanterer tap.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
Store tal
oktober 25, 2010 - 13:27 — Ragnar HaugeUngar som har lært å telja vert lett fascinert av store tal, og lurer på kva det største talet er. At det viser seg at det ikkje finst noko største tal er på same tid både naturleg og merkeleg ‑ naturleg av di ein alltid kan få eit større tal ved å leggja til 1, merkeleg av di det er svært vanskeleg å fatta det uendelege.
Så temaet her er framleis endelige, men store tal. Dersom ein ser på talorda peiker ein million seg ut som det første verkeleg store talet. Her oppstår det språkleg konvergens i dei fleste språk, med unntak av Aust-asia. Det heiter milyon i Adzerbajan, miloi på baskisk, miljoona på finsk, million på fransk, tysk og engelsk, milion på polsk, miliwn på walisisk, det er stort sett gjenkjenneleg.
Dette skuldast sjølvsagt til ein viss grad at det kjem frå det latinske mil, som artig nok tyder tusen, men språk som baskisk, ungarsk, finsk og walisisk låner vanligvis lite herifrå. Det verkar naturleg at når behovet for så store tal meldte seg, var det for dei fleste språk like greit å berre låna eit ord som allereie var i bruk. Sjølve ordet million dukka opp på 1200-talet.
Så på millionen er alle like og forstår kvarandre. Det vert raskt verre. Alle språk som har million har også billion, men no meiner ein ikkje lenger det same. I enkelte land vil ein billion vera tusen millionar, medan den i andre land er ein million millionar. Engelskspråklege land nyttar stort sett billion som tusen millionar, ein praksis som har utspring i USA, og vart generelt adoptert i alle formar av engelsk på 1970-talet. Brasil, austlege delar av Europa, Russland og ein del tidlegare sovjetrepublikkar og Indonesia nyttar også dette systemet.
Her til lands nyttar vi billion for ein million millionar, og har, som dei fleste andre land som tel på denne måten, ordet milliard for tusen millionar. Vi har så billiard for tusen billionar, trillion for tusen billiardar, og trilliard for tusen trillionar.
Prefiksa for tala etter milliard kjem også frå latin, men no startar ein å telja frå starten, med bi for 2, tri for 3, qua for 4 og så vidare. I vår notasjon vil tal som sluttar på -illion (og er større enn million) representera talet 10^6n, der n er det latinske talet som tilsvarer forstavinga. Ein kvintillion er dermed 1030, sidan kvint=5. 1000 kvintillionar er så ein kvintilliard, i tråd med million-milliard systemet.
Opp til centillion, som er 10600 (cent=100) fungerer dette greit nok, men det vert litt problematisk når ein kjem til 106000. Her får vi n=1000, og 1000 er mil på latin, så systemet gir talordet million, men det er allereie brukt. Millinillion er forselått for å løysa dette, men dei færraste ser trangen til å løysa dette problemet. Dette er absurd store tal, som ein nesten aldri vil klare å få bruk for, og om ein gjer det, held det lenge med "10 i sekstusende".
Det største talet som har spela ei anna rolle enn berre å vera eit eksempel på eit stort tal er Skewes tal, som dukka opp i eit matematisk prov frå 1933. Sjølve problemet dreier seg om ein funksjon som tel omtrent kor mange primtal det finst under ei gitt grense. For alle rimelege tal gir denne funksjonen eit litt for høgt tal, men Skewes viste at innan ein kom til 10^10^10^34 ville ein finna tal der funksjonen underestimerer kor mange primtal det er. Dette er eit bisarrt stort tal, grotesk mykje større enn den ovanfor nevnte millinillionen.
For dei som verkeleg er ute etter store tal er utfordringa å finna ein notasjon som kan skriva dei. Dette er ein sport for spesielt interesserte; min nevø i 4. klasse har framleis fullstendig overtaket på alle klassekameratane med sin centilliard når dei konkurrerer om store tal.
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |






