Uløselig matematikkoppgave?
juni 25, 2010 - 13:54 — Anne Randi Syvers...Min sønn i 5. klasse kom hjem fra skolen og var temmelig oppgitt over en matematikkprøve. En av oppgavene var uløselig, mente han. Oppgaven var som følger:
“Martin feirer bursdag. Gjestene kan velge mellom flere ting å spise.
12 ville ha sjokoladekake.
Halvparten av dem ville ha is.
10 flere enn dem som ville ha is, ville ha pannekaker.
Hvor mange gjester var det?”
Jeg måtte si meg enig i at dette ikke var løsbart, for som min sønn argumenterte: Halvparten pluss halvparten pluss 10 blir jo mer enn alle gjestene. Jeg antok at han hadde tolket oppgaven feil. Det stod for eksempel ikke noe tom at gjestene kunne velge bare en ting hver. Hvis halvparten av de som ville ha sjokoladekake i tillegg fikk is, ville dette gå bra, og antall gjester blir 12+16=28.
Løsningen kom da prøven ble delt ut igjen, ferdig rettet. Min sønns forklaring om at dette var uløselig, ble ikke godtatt som rett svar. Vi hadde tolket oppgaven feil. “Halvparten av dem” skulle bety halvparten så mange som de som hadde valgt sjokoladekake, altså 6, og antall gjester skulle bli 12+6+16=34.
Konklusjon: Presis språkbruk er viktig! Det er ikke alltid mottakeren oppfatter det du ønsker å kommunisere.
| Anne Randi Syversveen |
Jeg er utdannet sivilingeniør i industriell matematikk og doktor ingeniør i statistikk ved NTNU, Trondheim. Jeg har jobbet ved NR siden 1998. Jeg jobber med oljerelaterte problemstillinger, med vekt på 3D modellering av geologi. Fritiden min fylles av tre aktive barn som skal følges opp diverse aktiviteter. Dette har gitt meg arbeidsoppgaver i to idrettslag. Jeg liker å trene selv også når jeg har tid. Da tar jeg joggeskoene eller skiene med til skogs. |
Hva skjedde med Spania?
juni 22, 2010 - 11:55 — Anders LølandFør VM regnet NR ut at Spania hadde 21% sjanse for å vinne fotball-VM. Etter at alle gruppene har gjennomført to av tre runder, har det skjedd mye.
La oss gå rett på sak. Figuren under viser sannsynligheten for 1. plass for de tolv nåværende favorittene per i dag, etter kampene spilt 21. juni, samt utviklingen i vinnersannsynlighetene siden VM startet.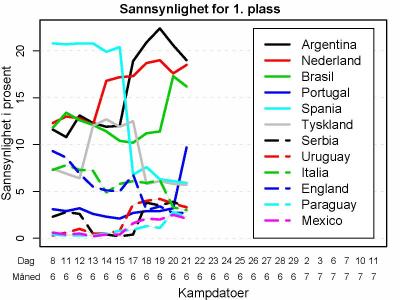
Mens Spania var favoritten og har rotet det til, er nå Argentina, Nederland og Brasil de tre klart største favorittene til å vinne VM. Sannsynligheten er nå over 50% prosent for at et av disse tre landene stikker av med pokalen. Dette er en konsekvens av kampene som er spilt så langt.
Det var noe skepsis til Argentina før VM, men etter to klare seire har de klatret til topps så langt.
Tyskland startet med en vinnersjanse på 7,5%. Den økte til rundt 12% etter den første seieren mot Australia, men falt igjen etter tapet mot Serbia.
Bakfra kommer Uruguay, Paraguay og Mexico, som har styrket sine sjanser betraktelig etter forhåndstipset på cirka 0,5%.
Beregningene er basert på at hvert lag tilordnes et styrketall før hver kamp. Ut fra styrketallene til to lag som møtes, skal en kunne avlese sannsynligheten for seier, uavgjort og tap. Styrketallene vil være noe à la FIFA-rankingen, men mer direkte relatert til utfallet av enkeltkamper.
Argentina, Nederland og Brasil har nå omtrent samme styrketall. Det betyr at NR-modellen mener de nå er omtrent like gode lag. Tilsvarende har Spania litt høyere styrketall enn Portugal, men lavere sannsynlighet for å vinne (9,5% mot 6%), siden Portugal i praksis er klare for åttendelsfinalen, mens Spania må vinne kampen mot Chile.
Modellen var før VM basert på tipsene til 14 fotballeksperter fra TV 2 Sporten. Eksperttipsene og de virkelige kampene blir vektet i forhold til hverandre, slik at eksperttipsene har like stor betydning som de virkelige kampene etter at hvert lag har spilt to kamper. Når alle lag har spilt flere enn to kamper betyr derimot de virkelige kampene mest.
Sannsynlighetene oppdateres hver dag under hele VM basert på kampene som blir spilt, og her kan det som vi har sett endre seg fort. Følg med videre på vm.nr.no!
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
For få frisparkmål i VM?
juni 21, 2010 - 11:53 — Anders LølandTil tross for 53 forsøk, har det hittil i VM ikke blitt scoret mål på direkte frispark. Skyldes dette JABULANI, den mye omtalte ballen, eller er det bare tilfeldighetene som er ute og går?
Ifølge en dokumentar sendt på britiske ITV har det i gjennomsnitt blitt mål på hvert 20. frispark i tidligere fotball-VM. Derfor burde vi sett minst to frisparkmål allerede. Men så har vi disse tilfeldighetene da.
Hvis vi går litt vitenskapelig til verks kan vi sette opp følgende påstand:
Det blir i gjennomsnitt mål på hvert 20. frispark.
Det betyr at sannsynligheten for mål er 5% per frispark. Vi antar her at hvert frispark er uavhengig av alle andre frispark.
Siden jeg som statistiker ikke kan fri meg fra å tro at dette kan skyldes tilfeldigheter, vil jeg ikke gi slipp på at hvert 20. frispark gir mål før sannsynligheten for at det er tilfeldig er under 5%, noe den ikke er ennå.
Først etter 59 frispark uten mål kan vi si at dette ikke er tilfeldig, og at det scores uvanlig få frisparkmål i årets VM. Det kan med andre ord skyldes tilfeldigheter, men er helt på grensen.
Det kan komme av JABULANI, men det finnes selvfølgelig andre muligheter. For eksempel kan det være de fæle VUVUZELAene som gjør frisparkerne mo i knærne!
For de spesielt interesserte kan jeg røpe at hvis jeg er strengere, og krever at sannsynligheten for at manglende frisparkmål skyldes tilfeldigheter er under 1%, er det først etter 91 frispark uten frisparkmål jeg med god samvittighet kan skylde på JABULANI eller noe annet.
Dette innlegget ble skrevet rett etter Italias trasige 1-1-kamp mot New Zealand på søndag. Følg med på http://vm.nr.no/ for oppdaterte sannsynligheter for de ulike lagenes plasseringer.
| Anders Løland |
Foto: Lin Stenstrud Jeg tok hovedfag i anvendt og industriell matematikk på Blindern i 1999, og jobbet deretter i et par år med sonardata ved Forsvarets forskningsinstitutt (FFI) på Kjeller. Siden 2001 har jeg jobbet ved NR. På fritida liker jeg å løpe oppover bratte bakker. Jeg heier på Hønefoss, som kommer til å imponere i eliteserien i år. |
Hyttepine
juni 18, 2010 - 10:36 — Ragnar HaugeGårsdagens Aftenposten tar for seg kostnadene ved å ha hytte. Dette vert forsøkt illustrert med eit reknestykke der dei samanliknar ein person som kjøper ei hytte for 2,5 millionar med ein som set tilsvarande beløp i banken. Imidlertid viser reknestykket at personen som kjøpte hytta lånte heile summen, medan den som sette dei på konto hadde dei tilgjengeleg. At det er betre å ha 2,5 millionar enn ikkje å ha det, er neppe overraskande - uavhengig av hyttekjøp.
| Ragnar Hauge |
Eg har jobba på Norsk Regnesentral sidan 1995. Mesteparten av tida har eg jobba med modellering av bergartar i oljereserervoar, men eg har etterkvart også mykje erfaring med bruk av seismiske data. Ut over det faglege er eg interessert i det aller meste, i alle fall frå eit teoretisk synspunkt. |
Stokastisk modellering av oljereservoarer
juni 11, 2010 - 13:45 — Anne Randi Syvers...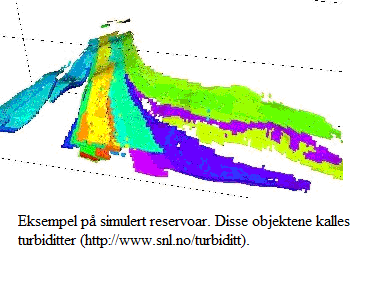 Før et oljereservoar kan utvinnes, må berggrunnen kartlegges på en best mulig måte. For å kunne ta ut olje, må berggrunnen være slik at oljen kan flyte gjennom den. Jo bedre flytegenskaper reservoaret har, jo større del av oljen i reservoaret kan utvinnes.
Før et oljereservoar kan utvinnes, må berggrunnen kartlegges på en best mulig måte. For å kunne ta ut olje, må berggrunnen være slik at oljen kan flyte gjennom den. Jo bedre flytegenskaper reservoaret har, jo større del av oljen i reservoaret kan utvinnes.
Det er utfordrende å finne ut hvordan berggrunnen ser ut under havbunnen. Berggrunnen består oftest av flere ulike steintyper, med ulike flytegenskaper. Geologene bygger modeller av bergartssammensetningen basert på kunnskap de har om området og lignende områder. De kan også ha data fra seismiske undersøkelser og brønner som allerede er boret. Men usikkerheten vil alltid være stor.
Vi på Norsk Regnesentral har utviklet dataverktøy for geologer basert på stokastiske modeller. Verktøyet lager 3D-modeller av oljereservoaret. Hver enkelt bergart blir modellert som objekter i en bakgrunn. Geologen kan legge inn den informasjonen han ønsker om for eksempel størrelsen på objektene, hvor mange 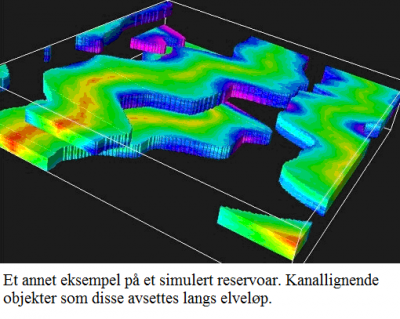 objekter, hvor stor andel det skal være av hver bergart, osv. Og han legger også inn hvor stor usikkerhet han tror det er i anslagene sine. Observasjoner fra brønner og seismikk legges inn i tillegg.
objekter, hvor stor andel det skal være av hver bergart, osv. Og han legger også inn hvor stor usikkerhet han tror det er i anslagene sine. Observasjoner fra brønner og seismikk legges inn i tillegg.
Ved hjelp av denne modellen simuleres et tenkt oljereservoar ut fra de opplysninger og den usikkerhet som er oppgitt. Ved å simulere mange reservoarer kan geologen få et inntrykk av den totale variasjonen i hvordan reservoaret kan se ut.
| Anne Randi Syversveen |
Jeg er utdannet sivilingeniør i industriell matematikk og doktor ingeniør i statistikk ved NTNU, Trondheim. Jeg har jobbet ved NR siden 1998. Jeg jobber med oljerelaterte problemstillinger, med vekt på 3D modellering av geologi. Fritiden min fylles av tre aktive barn som skal følges opp diverse aktiviteter. Dette har gitt meg arbeidsoppgaver i to idrettslag. Jeg liker å trene selv også når jeg har tid. Da tar jeg joggeskoene eller skiene med til skogs. |




